旅游公司租车问题 —— 动态规划 v.s. + Leapms线性规划

标签：数学   .com   ...   load   线性规划   span   库存   目标   bsp   

有一个旅游公司承包一条旅游线路，未来四周内的大巴车需求分别是：4辆、1辆、4辆和5辆。该公司向租车公司租赁服务，租车公司的计价方案是：租车收取一次性手续费3000，每车每周费用2000。求最节省租车方案。

线性规划方法

参数定义：

         d[k]: 第k周的需求车数；

         s[k]: 第k周周初库存车辆数量；

         x[k]: 第k周周初租车数量；

         y[k]第k周周初还车数量。

目标

   数学式：

       $\min \sum_{k=1}^{n}(3000x_k+2000(x_k+s_k-y_k))$

   +Leapms形式: 

       min sum{k=1,...,n}(3000x[k]+2000(x[k]+s[k]-y[k]))

 约束(+Leapms形式）： 

        s[k]+x[k]-y[k] ≥ d[k] | k=1,...,n                // 每周车辆需求约束
        s[k+1] =s[k] + x[k] - y[k] | k=1,...,n-1        //库存变化逻辑

数据：

         n=4
         d={4 1 4 5}

 完整+Leapms模型：

min sum{k=1,...,n}(5000x[k]+2000(s[k]-y[k]))
subject to
	x[k]+s[k]-y[k]>=d[k]| k=1,...,n
	s[k+1]=x[k]+s[k]-y[k]| k=1,...,n-1
	s[1]=0
where
	n is a number
	d is a set
	x[k],s[k],y[k] are variables of nonnegative numbers -->
		|k=1,...,n
data
	n=4
	d={4 1 4 5} 

在 +Leapms 中使用 load 和 mip 命令求解。

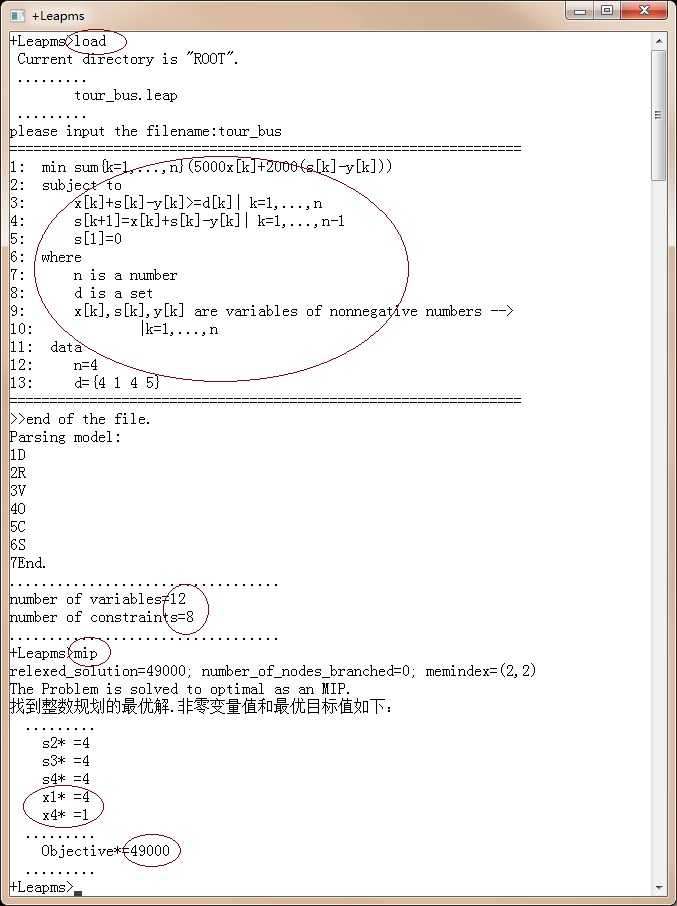
 得到最优解： x₁*=4, x₄*=1, x₂*=x₃*=0, 目标函数值：49000。

动态规划方法：

d_k: 第k周的需求车数；s_k : 第k周周初库存车辆数量；x_k: 第k周周初租车数量；y_k第k周周初还车数量。

递推方程：

                    f(s_k)=min{3000x_k+2000(s_k-y_k)+f(s_k+1)),    （1）

                    其中 s_k+1=s_k+x_k-y_k,                                   （2）

                           s_k+1≥d_k,                                             （3）

                           x_k≥0, y_k≥0。                                       （4）

动态规划递推：

    k=4时： s₅=d₄=5, 由（2）知道 5=s₄+x₄-y₄, 即：y₄=s₄+x₄-5，代入（1）:

                  f(s₄)=min{3000x₄+2000(5-x₄)+0}    →  f*(s₄) = 10000, x₄*=0

    k=3时：x3与y3只有一个为0, 且 s₃+x₃-y₃≥d₃=4 .

                  f₃(0)=min{3000x₃+2000(0-y₃)+10000}  →  f₃(0)* = 22000, x₃*=4, y₃*=0

　　　　    f₃(1)=min{3000x₃+2000(1-y₃)+10000}  →  f₃(1)* = 21000, x₃*=3, y₃*=0

　　　　    f₃(2)=min{3000x₃+2000(2-y₃)+10000}  →  f₃(2)* = 20000, x₃*=2, y₃*=0

 　　　　   f₃(3)=min{3000x₃+2000(3-y₃)+10000}  →  f₃(3)* = 19000, x₃*=1, y₃*=0

 　　　　   f₃(4)=min{3000x₃+2000(4-y₃)+10000}  →  f₃(4)* = 18000, x₃*=0, y₃*=0

  　　　　  f₃(5)=min{3000x₃+2000(5-y₃)+10000}  →  f₃(5)* = 18000, x₃*=0, y₃*=1

   k=2时：x2与y2只有一个为0, 且 s₂+x₂-y₂≥d₂=1 .

               f₂(0)=min{3000x₂+2000(0-y₂)+f₃(0+x₂-y₂)}  →  f₂(0)* = 24000, x₂*=1, y₂*=0

               f₂(1)=min{3000x₂+2000(1-y₂)+f₃(1+x₂-y₂)}  →  f₂(1)* = 25000, x₂*=1, y₂*=0

               f₂(2)=min{3000x₂+2000(1-y₂)+f₃(1+x₂-y₂)}  →  f₂(1)* = 25000, x₂*=1, y₂*=0

                   ...

 <非常繁琐> 。。。

  得到同样最优解： x₁*=4, x₄*=1, x₂*=x₃*=0, 目标函数值：49000。

旅游公司租车问题 —— 动态规划 v.s. + Leapms线性规划

标签：数学   .com   ...   load   线性规划   span   库存   目标   bsp   

原文地址：https://www.cnblogs.com/leapms/p/10045681.html