「PKUSC2018」神仙的游戏

标签：不同   经典   字符串匹配   ret   截图   ceil   出现   html   getch   

题目链接

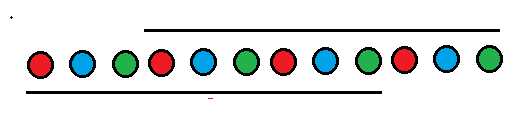
比如说上面\(|S|\)为12的字符串，我们欲求出\(f(9)\)的值，那么上面相同颜色的字符必须两两能够匹配。也就是说，同种颜色的字符集里不能同时出现0和1。如果只考虑同种颜色集里相邻的两个字符能否匹配，那么小样例都过不了。。

我们仔细观察就会发现，每隔\(|S|-len\)的位置就会出现相同的字符。我们可以认为长度为\(len\)的border实质上就是将长度为\(len\)的前缀向后偏移\(|S|-len\)，看是否能匹配。

如果有两个字符\(s[i],s[j]\ (i<j)\)，他们一个是0，一个是1，那么偏移量就不能为\(j-i\)。于是我们定义一个数组\(illegal\)。\(illegal[i]\)为1表示偏移量为\(i\)时不合法。

假设我们已经求出了\(illegal\)数组，我们判断\(f(len)\)的值，那么我们只需判断\(illegal[|S|-len]\)就可以了吗？当然不行，因为我们说了是字符集中不同时出现0和1，只判断\(illegal[|S|-len]\)相当于只判断了相邻两个字符能否匹配。所以我们还要判断\(|S|-len\)的倍数。

至于求\(illegal\)，就是经典的\(FFT/NTT\)在字符串匹配中的引用。可以构造一个反串，然后正反串做\(NTT\)就可以了。具体可以参考【BZOJ4259】残缺的字符串。

不过似乎不用这么麻烦，就直接将正串的1设为1，反串的0设为1然后一边\(NTT\)就行了。。

代码：

#include<bits/stdc++.h>
#define ll long long
#define N 500005
#define Z complex<double>
#define pi acos(-1)
#define mod 998244353

using namespace std;
inline int Get() {int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}while('0'<=ch&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}return x*f;}

char s[N];
int rev[N<<2],n;
ll f[N<<2],g[N<<2];
ll Match[N<<2];

ll ksm(ll t,ll x) {
    ll ans=1;
    for(;x;x>>=1,t=t*t%mod)
        if(x&1) ans=ans*t%mod;
    return ans;
}
void NTT(ll *a,int d,int flag) {
    static const ll G=3;
    int n=1<<d;
    for(int i=0;i<n;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<d-1);
    for(int i=0;i<n;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
    for(int s=1;s<=d;s++) {
        int len=1<<s,mid=len>>1;
        ll w=flag==1?ksm(G,(mod-1)/len):ksm(G,mod-1-(mod-1)/len);
        for(int i=0;i<n;i+=len) {
            ll t=1;
            for(int j=0;j<mid;j++,t=t*w%mod) {
                ll u=a[i+j],v=a[i+j+mid]*t%mod;
                a[i+j]=(u+v)%mod;
                a[i+j+mid]=(u-v+mod)%mod;
            }
        }
    }
    if(flag==-1) {
        ll inv=ksm(n,mod-2);
        for(int i=0;i<n;i++) a[i]=a[i]*inv%mod;
    }
}
bool illegal[N<<2];
ll ans;
int main() {
    scanf("%s",s+1);
    n=strlen(s+1);
    int d=ceil(log2(n*2+2));
    
    for(int i=1;i<=n;i++) {
        if(s[i]=='?') f[i]=g[n+1-i]=0;
        else if(s[i]=='0') {
            f[i]=g[n+1-i]=1;
        } else {
            f[i]=8,g[n+1-i]=2;
        }
    }
    
    NTT(f,d,1),NTT(g,d,1);
    for(int i=0;i<(1<<d);i++) f[i]*=g[i];
    NTT(f,d,-1);
    
    for(int i=0;i<(1<<d);i++) Match[i]+=f[i];
    memset(f,0,sizeof(f));
    memset(g,0,sizeof(g));
    for(int i=1;i<=n;i++) {
        if(s[i]=='?') f[i]=g[n+1-i]=0;
        else if(s[i]=='0') {
            f[i]=g[n+1-i]=1;
        } else {
            f[i]=4,g[n+1-i]=4;
        }
    }
    NTT(f,d,1),NTT(g,d,1);
    for(int i=0;i<(1<<d);i++) f[i]*=g[i];
    NTT(f,d,-1);
    for(int i=0;i<(1<<d);i++) Match[i]-=2*f[i];
    memset(f,0,sizeof(f));
    memset(g,0,sizeof(g));
    for(int i=1;i<=n;i++) {
        if(s[i]=='?') f[i]=g[n+1-i]=0;
        else if(s[i]=='0') {
            f[i]=g[n+1-i]=1;
        } else {
            f[i]=2,g[n+1-i]=8;
        }
    }
    NTT(f,d,1),NTT(g,d,1);
    for(int i=0;i<(1<<d);i++) f[i]*=g[i];
    NTT(f,d,-1);
    for(int i=0;i<(1<<d);i++) Match[i]+=f[i];
    
    for(int i=0;i<=n+1;i++) 
        if(Match[i]) illegal[abs(i-n-1)]=1;
    for(int i=1;i<=n;i++) {
        int flag=0;
        for(int j=i;j<=n;j+=i) {
            if(illegal[j]) {
                flag=1;
                break;
            }
        }
        if(!flag) ans^=1ll*(n-i)*(n-i);
    }
    ans^=1ll*n*n;
    cout<<ans;
    return 0;
}

「PKUSC2018」神仙的游戏

标签：不同   经典   字符串匹配   ret   截图   ceil   出现   html   getch   

原文地址：https://www.cnblogs.com/hchhch233/p/10048261.html