ARGMAX(以及ARGMIN)的意思

标签：数学   argmin   argmax   arg max   arg min   

1. argmax: argumentum maximi

论证最大？

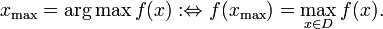
个人理解就是 以argmax取最大值时 将变量的取值赋值给式子

反之就是argmin

例子如下

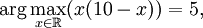
括号中f（x）的最大值为25， 此时变量x取值为5，将其赋值给式子，得到式子的结果为5

但据folie上的一些例子 可以有其他用法

比如想确定一个所需的y值 但取y值的时候需要考虑到x的取值情况 

也就是用y去代替前面式子里的x(max) 这也是可行的

例如找出f(x)最大的值时 y的取值

可以用argmax(f(x))作为所谓的"依据"

我想 这也是为什么字面翻译叫"论证最大（最小）"的原因吧

希望我没理解错。。。 中文wiki没有这个好像 我也不知道中文这个叫啥 没法查

至少目前套用到FOLIE上是对的~

2. ARG MIN的含义是什么？

最通俗的理解：表示使目标函数取最小值时的变量值
From Wikipedia

In mathematics, arg max (or argmax) stands for the argument of the maximum, that is to say, the set of points of the given argument for which the value of the given expression attains its maximum value:^{[note 1]}

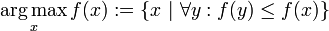
In other words,

is the set of values of x for which f(x) has the largest value M. For example, if f(x) is 1|x|, then it attains its maximum value of 1 at x = 0 and only there, so .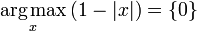

Equivalently, if M is the maximum of f, then the arg max is the level set of the maximum:

If the maximum is reached at a single value, then one refers to the point as the arg max, meaning we define the arg max as a point, not a set of points. So, for example,

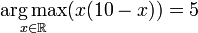
(rather than the singleton set {5}), since the maximum value of x(10  x) is 25, which happens when x = 5.^{[note 2]}

However, in case the maximum is reached at many values, arg max is a set of points.

Then, we have for example

since the maximum value of cos(x) is 1, which happens on this interval when x = 0, 2π or 4π. On the whole real line, the arg max is 

arg min (or argmin) is defined analogously.

Note also that functions do not in general attain a maximum value, and hence will in general not have an arg max: 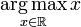 is undefined, as x isunbounded on the real line. However, by the extreme value theorem (or the classical compactness argument), a continuous function on a compact interval has a maximum, and thus an arg max.

1.  http://blog.163.com/htfei_1984/blog/static/677981242011445104058/

2. http://www.cppblog.com/guijie/archive/2010/12/13/136273.html

本文出自 “松鼠” 博客，请务必保留此出处http://apinetree.blog.51cto.com/714152/1563227

ARGMAX(以及ARGMIN)的意思

标签：数学   argmin   argmax   arg max   arg min   

原文地址：http://apinetree.blog.51cto.com/714152/1563227