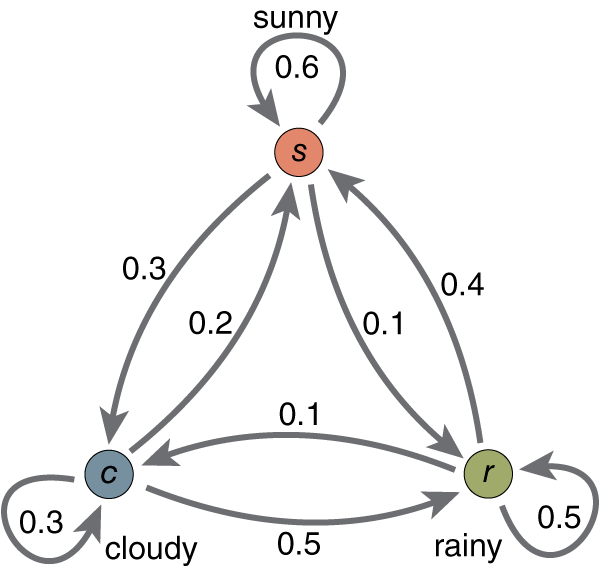
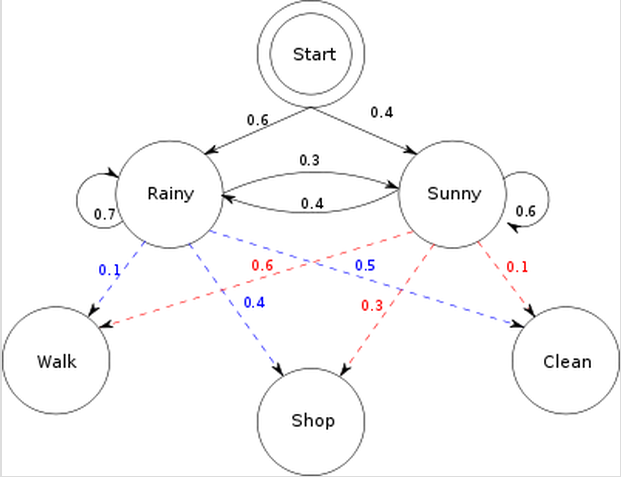
问题1的解决1：遍历算法。要计算产生这一系列行为的概率，那我们把每一种天气情况下产生这些行为都罗列出来，那每种情况的和就是这个概率。有三天，每天有两种可能的天气情况，则总共有 2的三次=8种 情况.
举例其中一种情况 ： P（下雨，下雨，下雨，散步，购物，收拾）=P（第一天下雨）P（第一天下雨去散步）P（第二天接着下雨）P（下雨去购物）P（第三天还下雨）P（下雨回家收拾）=0.6X0.1X0.7X0.4X0.7X0.5=0.00588
当然，这里面的 P（第二天接着下雨）当然是已知第一天下雨的情况下，第二天下雨的概率，为0.7.
将八种情况相加可得，三天的行为为{散步，购物，收拾}的可能性为0.033612. 看似简单易计算，但是一旦观察序列变长，计算量就会非常庞大（
的复杂度，T 为观测序列的长度）。
问题1 的解决2：向前算法。先计算 t=1时刻，发生『散步』一行为的概率，如果下雨，则为 P(散步，下雨)=P（第一天下雨）X P（散步 | 下雨）=0.6X0.1=0.06；晴天，P（散步，晴天）=0.4X0.6=0.24
t=2 时刻，发生『购物』的概率，当然，这个概率可以从 t=1 时刻计算而来。
如果t=2下雨，则 P（第一天散步，第二天购物， 第二天下雨）= 【P（第一天散步，第一天下雨）X P（第二天下雨 | 第一天下雨）+P（第一天散步，第一天晴天）X P(第二天下雨 | 第一天晴天)】X P（第二天购物 | 第二天下雨）=【0.06X0.7+0.24X0.3】X0.4=0.0552
如果 t=2晴天，则 P（第一天散步，第二天购物，第二天晴天）=0.0486 （同理可得，请自行推理）
如果 t=3，下雨，则 P（第一天散步，第二天购物，第三天收拾，第三天下雨）=【P（第一天散步，第二天购物，第二天下雨）X P（第三天下雨 | 第二天下雨）+ P（第一天散步，第二天购物，第二天天晴）X P（第三天下雨 | 第二天天晴）】X P（第三天收拾 | 第三天下雨）=【0.0552X0.7+0.0486X0.4】X0.5= 0.02904
如果t=3，晴天，则 P（第一天散步，第二天购物，第三天收拾，第三天晴天）= 0.004572
那么 P（第一天散步，第二天购物，第三天收拾），这一概率则是第三天，下雨和晴天两种情况的概率和。0.02904+0.004572=0.033612.
以上例子可以看出，向前算法计算了每个时间点时，每个状态的发生观测序列的概率，看似繁杂，但在 T 变大时，复杂度会大大降低。
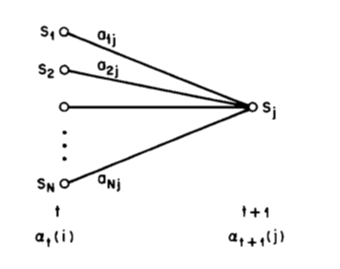问题1的解决3：向后算法顾名思义，向前算法是在时间 t=1的时候，一步一步往前计算。而相反的，向后算法则是倒退着，从最后一个状态开始，慢慢往后推。
初始化：
（第一次使用知乎的公式编辑，还蛮靠谱的嘛）
递推：
=0,.7x0.5x1+0.3x0.1x1=0.38
其中第一项则是转移概率，第二天下雨转到第三天下雨的概率为0.7；第二项则是观测概率，第三天下雨的状况下，在家收拾的概率为0.5；第三项就是我们定义的向后变量（backward variable）。
同理推得\beta_1(Rainy)=0.1298\\
\beta_1(Sunny)=0.1076" eeimg="1">
结束：P(散步，购物，收拾) =
=0.6×0.1×0.1298+0.4×0.6×0.1076
=0.033612
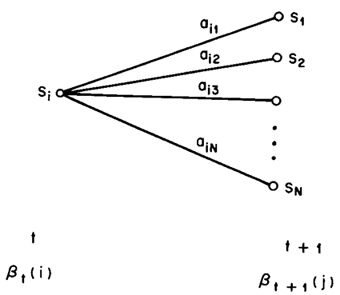
三种算法的答案是一致的。
问题2的解决：维特比算法
维特比算法致力于寻找一条最佳路径，以便能最好地解释观测到的序列。
初始化：\delta_1(Sunny)=\pi_S\times b_S(O_1=Walk)=0.24" eeimg="1">
初始路径：\phi_1(Sunny)=0" eeimg="1">
递推，当然是要找出概率比较大的那条路径。
那么，到达第二天下雨这一状态的最佳路径，应该是：
也就是说，第一天是晴天的可能性更大。
同样地，可以推得，\phi_2(Sunny)=Sunny\\
\delta_3(Rainy)=0.01344\\
\phi_3(Rainy)=Rainy\\
\delta_3(Sunny)=0.002592\\
\phi_3(Sunny)=Sunny
" eeimg="1">
结束：比较
的大小，发现前者较大，则最后一天的状态最有可能是 下雨天。
回推：根据
可知，到达第三天下雨这一状态，最有可能是第二天也下雨，再根据
可知，到达第二天下雨这一状态，最有可能是第一天是晴天。
由此，我们得到了最佳路径，即，晴天，雨天，雨天。
