标签:头结点 \n 最大 out 程序 搜索 注意 ret ace
1、基本思想:一个节点被访问后,它通过一系列的旋转,将节点放到树根上
2、展开:当一项x作为一片树叶被插入时,称为展开的一系列树的旋转使得x成为树的新根。
种类:
(1)x的父节点为根节点,直接单左(右)旋即可
(2)x有父亲(p)和祖父(g)
主要有三种旋转:单旋转,之字形旋转,一字型旋转。
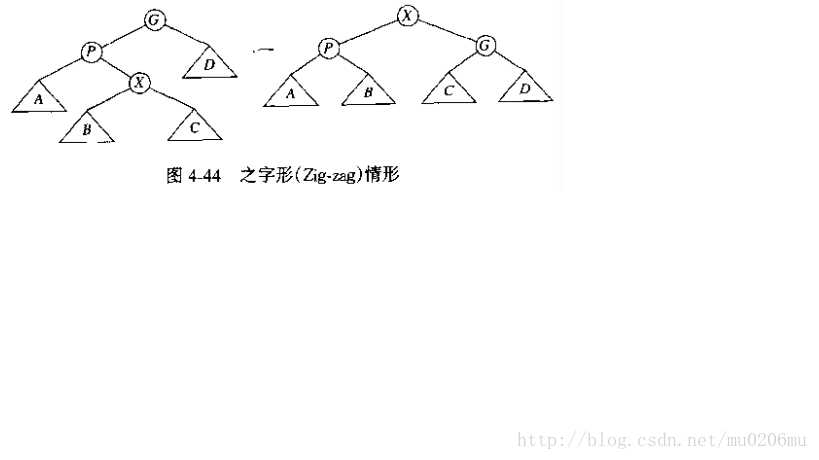
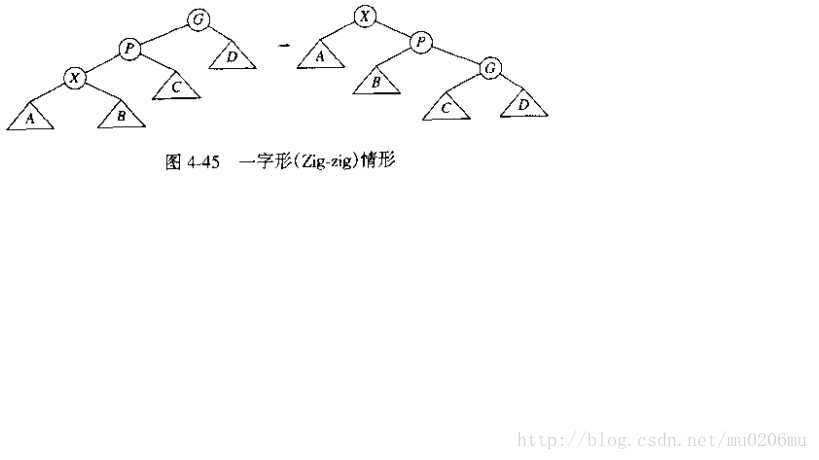
与搜索二叉树的结构体相同
(1)初始化:
通过建立一个静态全局变量NUllNode=NULL,标记一个NULL指针(可以简化程序)。
然后给NUllNode分配内存
SplayTree Init() { if(NUllNode==NULL) { NUllNode=(SplayNode)malloc(sizeof(struct Node)); if(NUllNode==NULL) printf("Out of Space!!!\n"); } return NUllNode; }
(2)伸展操作:
我们使用带有左指针和右指针的头结点最终包含左树的根后右树的根。
由于这两个树初始化为空,因此使用一个头结点对应状态右树或左树的最小或最大节点(避免检测空树)。
过程:
如果x小于当前节点的值,判断是否进行旋转,旋转完成后判断是否找到ITem节点,如果找到,就结束,没找到就进行将其右子树放到R上
如果x大于当前节点的值,判断是否进行旋转,旋转完成后判断是否找到Item节点,如果找到,就结束,没找到就进行将其左子树放到L上
每次变化L和R指针指向左子树的最大值或者右子树的最小值。
最后合并L,R和X子树(注意head的右节点记录的是L的右节点,head的左结点记录的是R的左结点)
SplayTree Splay(int Item,SplayTree X) { static struct Node head; SplayTree LeftTreeMax,RightTreeMin; head.Left=head.Right=NUllNode; LeftTreeMax=RightTreeMin=&head; NUllNode->data=Item; while(Item!=X->data) { if(Item<X->data) { if(Item<X->Left->data) X=SingleLeftRotate(X); if(X->Left==NUllNode) break; RightTreeMin->Left=X; RightTreeMin=X; X=X->Left; } else { if(Item>X->Left->data) X=SingleRightRotate(X); if(X->Right==NUllNode) break; LeftTreeMax->Right=X; LeftTreeMax=X; X=X->Right; } } LeftTreeMax->Right=X->Left; RightTreeMin->Left=X->Right; X->Left=head.Right; X->Right=head.Left; return X; }
(3)插入操作:
先建立一个新的节点,并对它初始化,如果是空树,直接插入即可
不是空树就先进行伸展操作,然后判断插入节点和根节点的
大小关系,
如果要插入节点的值小于根节点,原树的根节点和右子树变为新节点的右子树,原左子树变为新根节点的左子树;
如果要插入节点的值大于根节点,原树的根节点和左子树变为新节点的左子树,原右子树变为新根节点的右子树。
SplayTree Insert(int Item,SplayTree T) { static Position NewNode=NULL; if(NUllNode==NULL) { NUllNode=(SplayTree)malloc(sizeof(struct Node)); NUllNode->Left=NUllNode->Right=NULL; } NUllNode->data=Item; if(T==NULL) { NewNode->Left=NewNode->Right=NUllNode; T=NewNode; } else { T=Splay(Item,T); if(Item<T->data) { NewNode->Left=T->Left; NewNode->Right=T; T->Left=NUllNode; T=NewNode; } else if(Item>T->data) { NewNode->Right=T->Right; NewNode->Left=T; T->Right=NUllNode; T=NewNode; } else return T; } NewNode=NULL; return T; }
(4)删除操作:
如果不是空树,就通过一次伸展将要删除节点放到根上就行了,然后比较根与新节点的大小关系,
进行删除。
SplayTree Delete(int Item,SplayTree T) { SplayTree NewTree; if(T!=NUllNode) { T=Splay(Item,T); if(Item==T->data) { if(T->Left==NUllNode) NewTree=T->Right; else { NewTree=T->Left; NewTree=Splay(Item,NewTree); NewTree->Right=T->Right; } free(T); T=NewTree; } } return T; }
总代码:

#include<stdio.h> #include<stdlib.h> struct Node{ int data; struct Node *Left,*Right; }; typedef struct Node* SplayTree; typedef SplayTree Position; static SplayTree NUllNode=NULL; SplayTree Init() { if(NUllNode==NULL) { NUllNode=(SplayTree)malloc(sizeof(struct Node)); if(NUllNode==NULL) printf("Out of Space!!!\n"); NUllNode->Left=NUllNode->Right=NUllNode; } return NUllNode; } SplayTree MakeEmpty(SplayTree T) { if(T!=NULL) { MakeEmpty(T->Left); MakeEmpty(T->Right); free(T); } } SplayTree Find(int x,SplayTree T) { if(T==NULL) return NULL; if(x<T->data) return Find(x,T->Left); else if(x>T->data) return Find(x,T->Right); else return T; } SplayTree FindMin(SplayTree T) { if(T==NULL) return NULL; else if(T->Left==NULL) return T; else return FindMin(T); } SplayTree FindMax(SplayTree T) { if(T==NULL) return NULL; else if(T->Right==NULL) return T; else return FindMax(T); } SplayTree SingleLeftRotate(SplayTree T) { SplayTree tp=T->Left; T->Left=tp->Right; tp->Right=T; return tp; } SplayTree SingleRightRotate(SplayTree T) { SplayTree tp=T->Right; T->Right=tp->Left; tp->Left=T; return tp; } SplayTree Splay(int Item,SplayTree X) { static struct Node head; SplayTree LeftTreeMax,RightTreeMin; head.Left=head.Right=NUllNode; LeftTreeMax=RightTreeMin=&head; NUllNode->data=Item; while(Item!=X->data) { if(Item<X->data) { if(Item<X->Left->data) X=SingleLeftRotate(X); if(X->Left==NUllNode) break; RightTreeMin->Left=X; RightTreeMin=X; X=X->Left; } else { if(Item>X->Right->data) X=SingleRightRotate(X); if(X->Right==NUllNode) break; LeftTreeMax->Right=X; LeftTreeMax=X; X=X->Right; } } LeftTreeMax->Right=X->Left; RightTreeMin->Left=X->Right; X->Left=head.Right; X->Right=head.Left; return X; } SplayTree Insert(int Item,SplayTree T) { static Position NewNode=NULL; if(NewNode==NULL) { NewNode=(SplayTree)malloc(sizeof(struct Node)); if(NewNode==NULL) printf("Out of Space!!!\n"); } NewNode->data=Item; if(T==NUllNode) { NewNode->Left=NewNode->Right=NUllNode; T=NewNode; } else { T=Splay(Item,T); if(Item<T->data) { NewNode->Left=T->Left; NewNode->Right=T; T->Left=NUllNode; T=NewNode; } else if(Item>T->data) { NewNode->Right=T->Right; NewNode->Left=T; T->Right=NUllNode; T=NewNode; } else return T; } NewNode=NULL; return T; } SplayTree Remove(int Item,SplayTree T) { Position NewTree; if(T!=NUllNode) { T=Splay(Item,T); if(Item==T->data) { if(T->Left==NUllNode) NewTree=T->Right; else { NewTree=T->Left; NewTree=Splay(Item,NewTree); NewTree->Right=T->Right; } free(T); T=NewTree; } } return T; } void PreOrderTravel(SplayTree T) { if(T!=NUllNode) { printf("%d ",T->data); PreOrderTravel(T->Left); PreOrderTravel(T->Right); } } int main(void) { SplayTree T=Init(); int n,i,x; scanf("%d",&n); for(i=0;i<n;i++) { scanf("%d",&x); T=Insert(x,T); } PreOrderTravel(T); printf("\n"); T=Remove(3,T); PreOrderTravel(T); return 0; }
标签:头结点 \n 最大 out 程序 搜索 注意 ret ace
原文地址:https://www.cnblogs.com/2018zxy/p/10055335.html