标签:复制 初始 image 目的 pre 思想 步骤 free 要求
一、实验目的理解贪心法思想,掌握构造哈夫曼树的方法及哈夫曼编码的生成。
二、实验内容
按要求编写程序,次都选取未构造过的权值最小的叶子结点来构造哈夫曼树,最后根
据哈夫曼编码规则求出哈夫曼编码。 三、实验步骤步骤1:引入必要的函数库。
1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <string.h>
步骤2:定义结构体与别名。
1 typedef struct 2 { 3 int weight; //权值 4 int parent; //父结点序号 5 int left; //左子树序号 6 int right; //右子树序号 7 }HuffmanTree; 8 typedef char *HuffmanCode; //Huffman编码
步骤3:实现函数 SelectNode()。
函数作用:从 n 个结点中选择"parent 域取值为 0 且 weight 域取值小"的两个结点,并利用 参数 bt1,bt2 返回这两个结点在数组 ht[]中的下标。 参数含义: ht:指向 HuffmanTree 类型数组的首地址,该数组存放 n 个 HuffmanTree 类型结点,这
些结点对应于 Huffman 树中的叶结点或中间结点。 bt1,bt2:指针类型的参数,用于返回 HuffmanTree 类型数组 ht[]中"parent 域取值为零
且 weight 域取值最小"的两个结点的下标。 函数内部变含义:
ht1:保存数组 ht[]中"weight 域取值最小"的结点的内存地址。 ht1-ht:数组 ht[]中"weight 域取值最小"的结点在数组 ht 中的下标。 ht2:保存数组 ht[]中"weight 域取值次小"的结点的内存地址。
ht2-ht:数组 ht[]中"weight 域取值次小"的结点在数组 ht 中的下标。
1 void SelectNode(HuffmanTree *ht,int n,int *bt1,int *bt2) 2 { int i; 3 HuffmanTree *ht1,*ht2,*t; 4 ht1=ht2=NULL; //初始化两个结点为空 5 /*依次检查ht[]中的每个结点(包括叶结点和中间结点)。若当前结点ht[i]没有双亲, 则分以下情况进行处理:1)ht1取值为空。2)ht2取值为空。3)ht1与ht2取值为非空。*/ 6 for(i=1;i<=n;++i) 7 { if(!ht[i].parent) //父结点为空(结点的parent=0) 8 { if(ht1==NULL) //情况1:指针ht1为空 9 { 10 ht1=ht+i; //指向第i个结点,将其作为“当前weight域最小的”结点 11 continue; //退出当前轮次的for循环 12 } if(ht2==NULL) //情况2:指针ht2为空 13 { ht2=ht+i; //指向第i个结点 14 /*若ht2所指结点的weight域取值更小,则对换ht1与ht2,使得ht1 15 始终指向weight域取值更小的那个结点*/ 16 if(ht1->weight>ht2->weight) 17 { t=ht2; ht2=ht1; ht1=t; } continue; //退出当前轮次的for循环 18 } if(ht1 && ht2) //情况3:若ht1、ht2两个指针都有效 19 { 20 //第i个结点权重小于ht1指向的结点 if(ht[i].weight<=ht1->weight) 21 { 22 ht2=ht1; //ht2保存ht1,因为这时ht1指向的结点成为第2小的 23 ht1=ht+i; //ht1指向第i个结点 24 } 25 //若第i个结点权重小于ht2指向的结点 else if(ht[i].weight<ht2->weight){ 26 ht2=ht+i; //ht2指向第i个结点 27 } 28 } 29 } 30 } 31 /*对ht1与ht2进行比较,使得权值最小的两个结点按照它们在数组ht[]中最初的排列顺序出现。换言之,当两个权值相等时,使得Huffman树的左侧为叶结点,而不是中间结点(因为,叶结点在数组ht[]中的下标更小)*/ 32 if(ht1>ht2){ *bt2=ht1-ht; 33 *bt1=ht2-ht; 34 }else{ 35 *bt1=ht1-ht; 36 *bt2=ht2-ht; 37 } 38 }
步骤4:实现函数 CreateTree()。 函数作用:根据结点数组 ht[]和权重数组 w[],创建 Huffman 树。 参数含义: ht:HuffmanTree 类型数组的首地址。注意,在数组 ht[]中,单元 ht[0]并不使用,单元
ht[1..n]中存放的是叶结点,单元 ht[n+1..m]中存放的是中间结点。
n:数组的长度。
w:权重数组的首地址。
1 void CreateTree(HuffmanTree *ht,int n,int *w) 2 { 3 int i,m=2*n-1;//总的结点数量 4 int bt1,bt2; 5 if(n<=1) return ; //只有一个结点,无法创建 6 for(i=1;i<=n;++i) //初始化叶结点 7 { 8 ht[i].weight=w[i-1]; ht[i].parent=0; ht[i].left=0; ht[i].right=0; 9 } 10 for(;i<=m;++i)//初始化中间结点(数组ht[n+1..m]中保存的是中间结点) 11 { 12 ht[i].weight=0; ht[i].parent=0; ht[i].left=0; ht[i].right=0; 13 } 14 //逐个计算非叶结点的信息,创建Huffman树 15 for(i=n+1;i<=m;++i) 16 { 17 /*从数组ht[]的第1~i-1个单元中选择“parent域取值0且weight域取值最小”的两个结点,即ht[bt1]和ht[bt2]*/ 18 SelectNode(ht,i-1,&bt1,&bt2); 19 //将当前结点ht[i]作为结点ht[bt1]的双亲 20 ht[bt1].parent=i; 21 //将当前结点ht[i]作为结点ht[bt2]的双亲 22 ht[bt2].parent=i; 23 //将结点ht[bt1]作为当前结点ht[i]的左孩子 24 ht[i].left=bt1; 25 //将结点ht[bt2]作为当前结点ht[i]的右孩子 26 ht[i].right=bt2; 27 //根据左孩子ht[bt1]和右孩子ht[bt2]的weight域计算产生当前结点ht[i]的weight域 28 ht[i].weight=ht[bt1].weight+ht[bt2].weight; 29 } 30 }
步骤5:实现函数 HuffmanCoding()。 函数作用:根据 Huffman 树生成个字符的 Huffman 编码。 对于 i=1,...n,执行以下过程:
1)采用"自下而上"(即自叶至根)方式为数组 ht[]中的当前叶结点 ht[i]产生 Huffman 编码,所得编码临时存放在 cd[start..n-1]中。显然,该编码的长度为(n-1)-start+1=n-start 个字符。
2)动态分配长度为 n-start 个字节的内存,并且令字符指针 hc[i]指向这段空间的首地址。
3)将 cd[start..n-1]的内容复制到 hc[i]所指向的内存空间。
参数含义:
ht:HuffmanTree 类型数组的首地址
hc:根据"typedef char * HuffmanCode"可知,参数 hc 的类型为 char * *,即 hc 可以理
解为一个 char *类型数组的首地址。其中,单元 hc[0..n-1]中依次存放一个字符指针,且这些 字符指针分别指向所对应的叶结点的 Huffman 编码。具体地,hc[0]指向第一个叶结点的 Huffman 编码,hc[1]指向第一个叶结点的 Huffman 编码,以此类推。 函数内部变含义:
cd:长度为 n 的字符数组的首地址,其中,cd[n-1]=‘\0‘,且 cd[start..n-2]中存放了某个叶
结点的 Huffman 编码。
1 void HuffmanCoding(HuffmanTree *ht,int n,HuffmanCode *hc) 2 { 3 char *cd; 4 int start,i; 5 int current,parent; 6 //用来临时存放一个字符的编码结果 7 cd=(char*)malloc(sizeof(char)*n); 8 cd[n-1]=‘\0‘; //设置字符串结束标志 9 for(i=1;i<=n;i++) 10 { 11 start=n-1; 12 current=i; 13 parent=ht[current].parent;//获取当前结点的父结点 14 while(parent) //父结点不为空 15 { 16 if(current==ht[parent].left)//若该结点是父结点的左子树 17 cd[--start]=‘0‘; //编码为0 18 else //若结点是父结点的右子树 19 cd[--start]=‘1‘; //编码为1 20 current=parent; //设置当前结点指向父结点 21 parent=ht[parent].parent; //获取当前结点的父结点序号 22 } 23 hc[i-1]=(char*)malloc(sizeof(char)*(n-start));//分配保存编码的内存 24 strcpy(hc[i-1],&cd[start]); //复制生成的编码 25 } 26 free(cd); //释放编码占用的内存 27 }
步骤6:编写主函数 main()。
1 ht=(HuffmanTree *)malloc((m+1)*sizeof(HuffmanTree)); 2 if(!ht) 3 { 4 printf("内存分配失败!\n"); 5 exit(0); 6 } 7 /*申请内存,创建长度为n的字符指针数组,其中元素hc[i-1]指向第i个叶结点的 8 Huffman编码*/ 9 hc=(HuffmanCode *)malloc(n*sizeof(char*)); 10 if(!hc) 11 { 12 printf("内存分配失败!\n"); 13 exit(0); 14 } 15 CreateTree(ht,n,w); //利用n个叶结点和相关权重创建赫夫曼树 16 HuffmanCoding(ht,n,hc); //为每个叶结点(即字符)产生对应的赫夫曼编码 17 for(i=1;i<=n;i++) //输出每个叶结点(即字符)的赫夫曼编码 18 printf("字母:%c,权重:%d,编码为 %s\n",alphabet[i-1],ht[i].weight,hc[i-1]); 19 system("PAUSE"); 20 return 0; 21 }
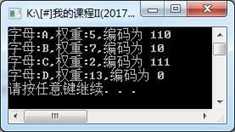
运行效果
标签:复制 初始 image 目的 pre 思想 步骤 free 要求
原文地址:https://www.cnblogs.com/lgqrlchinese/p/10066869.html