标签:lse nat 根据 如何 return 答案 col 并集 href
CF1059D Nature Reserve (精度处理,计算几何,二分)
题目链接:CF1059D
首先处理无解情况,如果在 $x$ 轴两侧都有点,则无解。
我们在将所有 $y$ 值都变为正数方便处理
如果圆与 $x$ 轴相切,则该圆的一条半径垂直于 $x$ 轴。
于是我们可以二分半径 $R$
那么圆心的纵坐标是确定的,那么我们如何判断该半径能否覆盖所有圆呢?
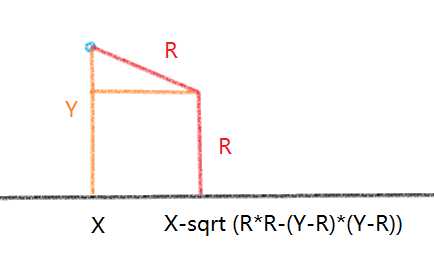
如图我们根据勾股定理算出圆心的 $横坐标$ 的的集合
我们可以算出 $X_圆$ $\le$ $X+\sqrt{R^{2}-(Y-R)^{2}} $ $ps$:上图有点 $bug$
$X_圆$ $\ge$ $X-\sqrt{R^{2}-(Y-R)^{2}} $
则所有点的并集为空则不成立,反之成立
以上写在 $check$ 函数中
然后就是二分答案
精度问题:
因为题目要求是与正确答案相对相差1e-6即可,所以我们将eps设为期望答案大小的1e-7被即可,防止超时,卡精度
1 #include<bits/stdc++.h> 2 #define MAXN 100010 3 using namespace std; 4 struct Point{ 5 int x,y; 6 }a[MAXN]; 7 int n; 8 bool f1,f2; 9 bool check (double k) 10 { 11 double L=-1e15,R=1e15; 12 for (int i=1;i<=n;i++) 13 { 14 double tmp=a[i].y*(2*k-a[i].y); 15 if (tmp<0) return 0; 16 tmp=sqrt (tmp); 17 L=max (L,a[i].x-tmp);R=min (R,a[i].x+tmp); 18 } 19 return L<=R; 20 } 21 int main() 22 { 23 scanf ("%d",&n); 24 int Min_B=1e9,Max_B=-1e9,High=-1e9; 25 for (int i=1;i<=n;i++) 26 { 27 scanf ("%d%d",&a[i].x,&a[i].y); 28 Min_B=min (Min_B,a[i].x); 29 Max_B=max (Max_B,a[i].x); 30 High=max (High,abs (a[i].y)); 31 if (a[i].y>0) f1=1; 32 if (a[i].y<0) f2=1; 33 } 34 if (f1&&f2) 35 { 36 printf ("-1"); 37 return 0; 38 } 39 if (f2) for (int i=1;i<=n;i++) a[i].y=-a[i].y; 40 double l=0,r=1e14; 41 double eps=max (High,(Max_B-Min_B))*1e-8; 42 while (r-l>eps) 43 { 44 double mid=(l+r)/2; 45 if (check (mid)) r=mid; 46 else l=mid; 47 } 48 printf ("%.7lf",r); 49 return 0; 50 }
CF1059D Nature Reserve (精度处理,计算几何,二分)
标签:lse nat 根据 如何 return 答案 col 并集 href
原文地址:https://www.cnblogs.com/PaulShi/p/10078337.html