标签：des style blog http color io os ar for
| Time Limit: 2000MS | Memory Limit: 30000K | |
| Total Submissions: 12521 | Accepted: 4524 | |
| Case Time Limit: 1000MS | ||
Description
Input
Output
Sample Input
2 3 2 0 3 2 1 1 3 0 3 2 0 2 3 0 1 0 1 2 1 0 2 1 0 0 2 0
Sample Output
2
题目意思：
有K个牛奶站（1--K），C个牛（K+1---C），牛和牛、牛和牛奶站、牛奶站和牛奶站之间有些边，所有的牛都需要到牛奶站，牛奶站最多容纳M个牛，求在满足题目条件下，所有的牛都到牛奶站所经过的最大路程中最小的。
思路：
假设输入的图如下：
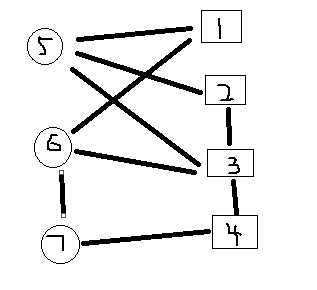其中圆代表牛，方块代表牛奶站。
易知若使得最大路程最小，那么该路径必须在某头牛与某个牛奶站之间的最短距离。
那么经过floyd求的牛与牛奶站之间的最短距离后，图如下：
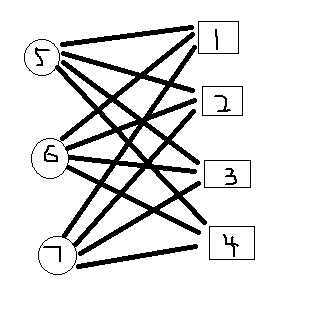此时图示路径都是最短路径，最大路径就在这些路径当中（设这些路径中最大为maxh），那么怎么找出来呢，就想到了对这些边二分查找(查找区间为[0,maxh],查找的边为最大边)，当查找到的这条最大边处于不超过所有牛奶站容量和超过某些牛奶站容量临界状态下，那么满足所有牛奶站容量的边即为答案。
那么又怎么判断当这条边为最大边时牛奶站容量是否超过最大容量呢？那么就有最大流了，虚拟一个源点，使得源点指向牛，虚拟一个汇点，使得牛奶站指向汇点，建图如下：
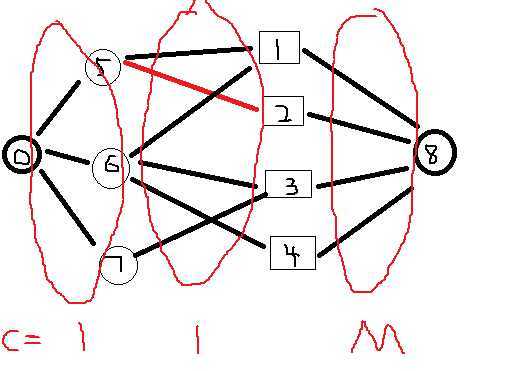其中红线为查找到的最大边，在第二边集中其他的边均小于红线。第一边集和第二边集边的容量为1，第三边集边的容量为M。
求的源点0到汇点8的最大流若为牛个数C的话说明不超过牛奶站容量。
经过上面分析就知道实现过程了：
先对输入的图进行floyd求最短路径，然后找出牛和牛奶站之间最大边maxh，从[0,maxh]中二分查找最大边，根据这个最大边从新建图，然后用最大流判断这条边是否满足不超过牛奶站容量的条件。
代码：
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <iostream> 5 #include <vector> 6 #include <queue> 7 using namespace std; 8 9 #define inf 9999999 10 11 vector<int>ve[6100]; 12 int map[240][240]; 13 int g[240][240]; 14 int flow[240], father[240]; 15 int K, C, M; 16 17 int build(int lim){ //建图，新图为g[][] 18 int i, j, k, maxh=-1; 19 memset(g,0,sizeof(g)); 20 for(i=K+1;i<=K+C;i++) g[0][i]=1; 21 for(i=1;i<=K;i++) g[i][K+C+1]=M; 22 for(i=K+1;i<=K+C;i++){ 23 for(j=1;j<=K;j++){ 24 if(map[i][j]<=lim){ 25 g[i][j]=1; 26 maxh=max(maxh,map[i][j]); 27 } 28 29 } 30 } 31 return maxh; 32 } 33 34 int bfs(){ //找增广路 35 int i, j, u, v; 36 queue<int>Q; 37 while(!Q.empty()) Q.pop(); 38 u=0; 39 memset(father,-1,sizeof(father)); 40 flow[u]=inf; 41 father[u]=0; 42 Q.push(u); 43 while(!Q.empty()){ 44 u=Q.front();Q.pop(); 45 for(v=1;v<=K+C+1;v++){ 46 if(father[v]==-1&&g[u][v]>0){ 47 flow[v]=min(flow[u],g[u][v]); 48 father[v]=u; 49 Q.push(v); 50 } 51 } 52 } 53 if(father[K+C+1]==-1) return -1; 54 return flow[K+C+1]; 55 } 56 57 int FLOW(){ //最大流 58 int i, j, step; 59 int ans=0; 60 while((step=bfs())!=-1){ 61 ans+=step; 62 int u=K+C+1; 63 while(u!=0){ 64 g[father[u]][u]-=step; 65 g[u][father[u]]+=step; 66 u=father[u]; 67 } 68 } 69 return ans; 70 } 71 72 main() 73 { 74 int i, j, k; 75 while(scanf("%d %d %d",&K,&C,&M)==3){ 76 for(i=1;i<=K+C;i++){ 77 for(j=1;j<=K+C;j++){ 78 scanf("%d",&map[i][j]); 79 if(!map[i][j]) map[i][j]=inf; 80 } 81 } 82 int minmax=-1; 83 for(k=1;k<=K+C;k++){ //floyd最短路径 84 for(i=1;i<=K+C;i++){ 85 for(j=1;j<=K+C;j++){ 86 map[i][j]=min(map[i][j],map[i][k]+map[k][j]); 87 if(map[i][j]<inf) minmax=max(minmax,map[i][j]); 88 } 89 } 90 } 91 int l=0, r=minmax, ans; 92 while(l<r){ //二分查找 93 int mid=(l+r)/2; 94 build(mid); //根据查找到的最大边mid从新建图 95 if(FLOW()>=C) r=mid; //最大流判断是否满足不超过牛奶站容量的条件 96 else l=mid+1; 97 } 98 ans=build(r); //查找的mid仅为最大边的上届，不一定是最大边，所以找最接近上届的边即为最大边 99 printf("%d\n",ans); 100 } 101 }
标签：des style blog http color io os ar for
原文地址：http://www.cnblogs.com/qq1012662902/p/4023350.html
