标签：概率   最优二叉树   图片   9.png   buffered   pack   setw   路径   编程   

Java哈夫曼编码实验--哈夫曼树的建立，编码与解码

建树，造树，编码，解码

一、哈夫曼树编码介绍

• 1、哈夫曼树：
  • （1）定义：假设有n个权值{w1, w2, ..., wn}，试构造一棵含有n个叶子结点的二叉树，每个叶子节点带权威wi，则其中带权路径长度WPL最小的二叉树叫做最优二叉树或者哈夫曼树。
  • （2）特点：哈夫曼树中没有度为1的结点，故由n0 = n2+1以及m= n0+n1+n2，n1=0可推出m=2*n0-1，即一棵有n个叶子节点的哈夫曼树共有2n-1个节点。
• 2、哈夫曼编码步骤：
  • （1）计算字符出现的次数：
    • 假设我们现在有一段文档需要进行编码，我们现在需要对于每一个字符出现的次数进行统计，然后分别计算出其在这篇文档的权重，也就是频率，我们用下面的一段文字进行举例；
    • 在如下的文档中包括的字符有8个字母和2个空格，所以我们现在需要去统计这10个字符的个数，统计后的数据如下：
  • （2）对字符出现的次数作为一个权重，从小到大进行排序；
    • 排序结果：0.1,0.1,0.1,0.1,0.1,0.1,0.2,0.2
  • （3）依照排序结果从小到大根据以下规则进行造树：
    • a、最小的前两个数进行权重的相加，形成他们两个作为左子树和右子树的父结点，如果是左结点就标记为0，如果是右结点就标记为1
    • b、然后将父结点作为一个新的结点进入排序结果，之后进行重新排序（ps：假如出现添加后的父结点的权重和之前排序中的结点的权重相等的情况，两者的位置具体是对于建树没有影响的，但是在编程实现的过程中，程序需要将两者的位置进行确定）
    • c、重复上述过程，直到得到的父结点的权重为1。
    • d、具体流程如下：

    i like you  //文档

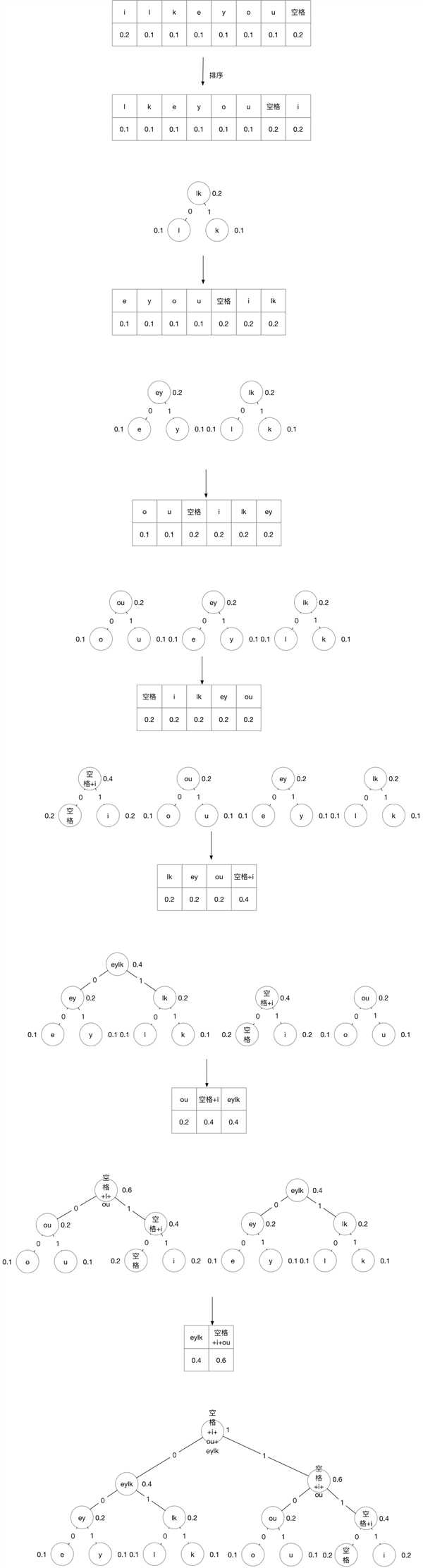
从根向下一次读取0或者1，进行编码，编码结果如下表

二、编程实现过程

• 1、首先我准备了一段英文文档，包括26个字母和一个空格字符

for many young people they dont have the habit to save money because they think they are young and should enjoy the life quickly so there is no need to save money but saving part of the income can better help us to deal with emergent situations though it is hard to store income index zero we still can figure out some ways

• 2、然后先进行文件的读取和进行字符出现的次数统计

  //读取文档中的英文文档
        String[] a = new String[800];
        try (FileReader reader = new FileReader("英文文档");
             BufferedReader br = new BufferedReader(reader)
        ) {
            int b =0;
            for (int i =0;i<800;i++){
                a[b]=br.readLine();
                b++;
            }
            } catch (IOException e) {
            e.printStackTrace();
        }
        String[] b = a[0].split("");
    //    System.out.println(Arrays.toString(b));
//开始构造哈夫曼树
          Objects Za= new Objects("a",an);
        Objects Zb = new Objects("b",bn);
        Objects Zc = new Objects("c",cn);
        Objects Zd = new Objects("d",dn);
        Objects Ze = new Objects("e",en);
        Objects Zf = new Objects("f",fn);
        Objects Zg = new Objects("g",gn);
        Objects Zh = new Objects("h",hn);
        Objects Zi = new Objects("i",in);
        Objects Zj = new Objects("j",jn);
        Objects Zk = new Objects("k",kn);
        Objects Zl = new Objects("l",ln);
        Objects Zm = new Objects("m",mn);
        Objects Zn = new Objects("n",nn);
        Objects Zo = new Objects("o",on);
        Objects Zp = new Objects("p",pn);
        Objects Zq = new Objects("q",qn);
        Objects Zr = new Objects("r",rn);
        Objects Zs = new Objects("s",sn);
        Objects Zt = new Objects("t",tn);
        Objects Zu = new Objects("u",un);
        Objects Zv = new Objects("v",vn);
        Objects Zw = new Objects("w",wn);
        Objects Zx = new Objects("x",xn);
        Objects Zy = new Objects("y",yn);
        Objects Zz = new Objects("z",zn);
        Objects Zkongge = new Objects(" ",zkongge);

        System.out.println("各个字符的概率统计为：");
        Objects[] temp = new Objects[]{Za,Zb,Zc,Zd,Ze,Zf,Zg,Zh,Zi,Zj,Zk,Zl,Zm,Zn,Zo,Zp,Zq,Zr,Zs,Zt,Zu,Zv,Zw,Zx,Zy,Zz,Zkongge};
            for (int i =0;i<temp.length;i++){
                System.out.println(temp[i].getName()+"的概率为"+temp[i].getWeight()/323);
            }

• 3、因为我用了一个Objects保存了一个元素的名字，权重，编码，还有他的左孩子,右孩子。

package 哈夫曼树编码实验;

public class Objects implements Comparable<Objects> {
    private String name;
    private double weight;
    private String date;
    private Objects left;
    private Objects right;
    public Objects(String Name , double Weight){
        name=Name;
        weight=Weight;
        date="";
    }
    public String getName() {
        return name;
    }

    public double getWeight() {
        return weight;
    }

    public Objects getLeft() {
        return left;
    }

    public Objects getRight() {
        return right;
    }

    public void setLeft(Objects left) {
        this.left = left;
    }

    public void setRight(Objects right) {
        this.right = right;
    }

    public void setName(String name) {
        this.name = name;
    }

    public void setWeight(double weight) {
        this.weight = weight;
    }

    @Override
    public String toString() {
        return "Objects{" + "name='" + name + '\'' + ", weight=" + weight + ", 编码为='" + date + '\'' + '}'+"\n";
    }

    @Override
    public int compareTo(Objects o) {
        if (weight>=o.weight){
            return 1;
        }
        else {
            return -1;        //规定发现权重相等向后放；
        }
    }

    public void setDate(String date) {
        this.date = date;
    }

    public String getDate() {
        return date;
    }
}

• 4、进行哈夫曼树的建立

 List tempp = new ArrayList();
        for (int i =0;i<temp.length;i++){
            tempp.add(temp[i]);
        }
        Collections.sort(tempp);        //将我们的Objects类中的每一个字符放进链表进行排序


        while (tempp.size() > 1) {            //直到我们链表只剩下一个元素，也就是我们的根结点的时候跳出循环
            Collections.sort(tempp);            //排序
            Objects left = (Objects) tempp.get(0);        //得到第一个元素，作为左孩子
            left.setDate( "0");    //初始化左孩子的编码为0
            Objects right = (Objects) tempp.get(1);    //得到第二个元素，作为右孩子
            right.setDate( "1");    //初始化有孩子的编码为1
            Objects parent = new Objects(left.getName()+right.getName(), left.getWeight() + right.getWeight());    //构造父结点
            parent.setLeft(left);    //设置左结点
            parent.setRight(right);    //设置右结点
            tempp.remove(left);    //删除左结点
            tempp.remove(right);    //删除右结点
            tempp.add(parent);    //将父结点添加进入链表
            }

• 5、开始进行编码

     //开始进行哈夫曼编码
        Objects root = (Objects) tempp.get(0);    //我们通过一个root保存为根结点

        System.out.println( );        //我们利用先序遍历，遍历到每一个结点，因为这样可以保证都从根结点开始遍历
        List list = new ArrayList();
        Queue queue = new ArrayDeque();
        queue.offer(root);
        while (!queue.isEmpty()){
            list.add(queue.peek());
            Objects temp1 = (Objects) queue.poll();

            if(temp1.getLeft() != null)
            {
                queue.offer(temp1.getLeft());
                temp1.getLeft().setDate(temp1.getDate()+"0");    //判断假如为左结点，就基于结点本身的编码加上0
                }

            if(temp1.getLeft() != null)
            {
                queue.offer(temp1.getRight());
                temp1.getRight().setDate(temp1.getDate()+"1");    //判断假如为右结点，就基于结点本身的编码加上1
            }
            }

• 6、开始对于文档进行加密并且保存进文档

 //进行加密
        String result = "";            //定义了一个字符串，用来保存加密后的文档
        for (int i =0 ;i<b.length;i++){
            for (int j=0;j<temp.length;j++){
                if (b[i].equals(temp[j].getName())){
                    result+=temp[j].getDate();        //因为现在我们之前保存Objects的数组中的每一个字符已经有各自的编码，所以我们用我们之前保存文档的数组b进行对于，假如找到相对应的，就将编码赋给result，进行累加，重复过程
                    break;                                            
                }

            }
        }
        System.out.println("加密后");
        System.out.println(result);
        File file = new File("加密后文档");
        FileWriter fileWritter = null;
        try {
            fileWritter = new FileWriter(file.getName(),true);
        } catch (IOException e) {
            e.printStackTrace();
        }
        try {
            fileWritter.write(result);
        } catch (IOException e) {
            e.printStackTrace();
        }
        try {
            fileWritter.close();
        } catch (IOException e) {
            e.printStackTrace();
        }

• 7、进行解密

  //解密，读取需要解密的文档
        try (FileReader reader = new FileReader("加密后文档");
             BufferedReader br = new BufferedReader(reader)
        ) {
            int e =0;
            for (int i =0;i<800;i++){
                a[e]=br.readLine();
                e++;
            }
        } catch (IOException e) {
            e.printStackTrace();
        }
        String duqu=a[0];    
        String jiemi="";    //保存解密后的文档
        String temp2="";   // 作为一个临时的字符串，一个一个进行获取密文，当进行匹配成功了以后，变为空，如下

        for (int i =0;i<duqu.length();i++){
            temp2+=duqu.charAt(i);
            for (int j = 0;j<temp.length;j++){            //这里解密的思路就是我们从加密的文档中一个一个字符进行获取，然后与我们的之前建好的Objects数组中的元素的编码
                if (temp2.equals(temp[j].getDate())){  //进行获取，然后获取成功以后将其赋给jiemi，然后清空temp2；
                    jiemi+=temp[j].getName();
                    temp2="";
                }
            }
        }
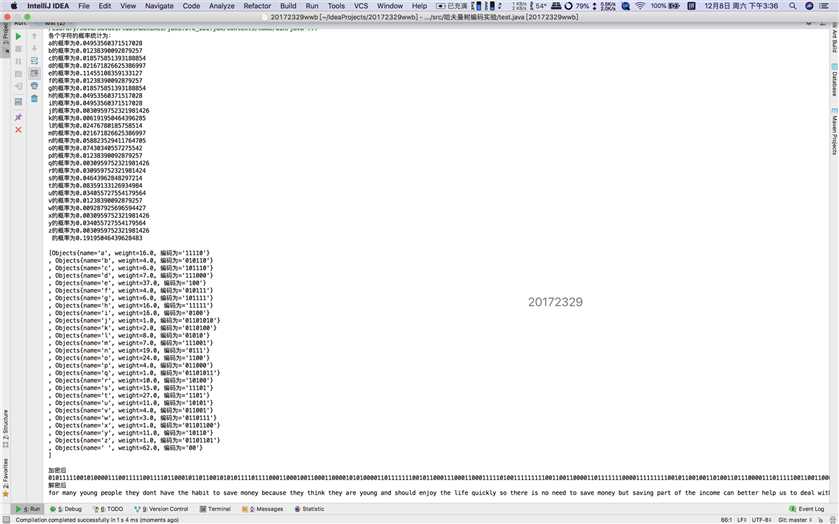
        System.out.println("解密后");
        System.out.println(jiemi);
        //将解密后的文本写入文件

        File file1 = new File("解密后文档");
        FileWriter fileWritter1 = null;
        try {
            fileWritter1 = new FileWriter(file1.getName(),true);
        } catch (IOException e) {
            e.printStackTrace();
        }
        try {
            fileWritter1.write(jiemi);
        } catch (IOException e) {
            e.printStackTrace();
        }
        try {
            fileWritter1.close();
        } catch (IOException e) {
            e.printStackTrace();
        }

• 8、成功完成加密解密，结果如下：
  

实验代码链接

参考资料

java创建哈夫曼树和实现哈夫曼编码

哈夫曼树的编码实验

标签：概率   最优二叉树   图片   9.png   buffered   pack   setw   路径   编程   

原文地址：https://www.cnblogs.com/qh45wangwenbin/p/10089416.html