最大熵模型

标签：nbsp   特征   拉格朗日对偶   算法   bsp   条件   假设   外部   目标   

最大熵原理

承认已知事物（知识），对未知事物不做任何假设，没有任何偏见

最大熵存在且唯一（凸性）

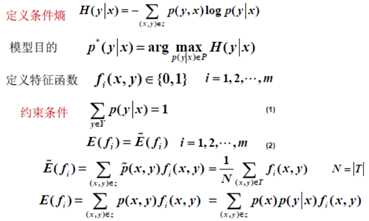
概率平均分布等价于熵最大

最大熵模型的一般式

关于条件分布 P(Y|X)的熵为：

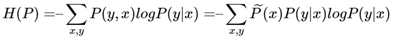
去掉负号，得到最大熵模型的等价式

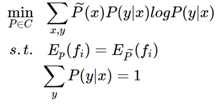
MaxEnt 模型最后被形式化为带有约束条件的最优化问题，可以通过拉格朗日乘子法将其转为无约束优化的问题，引入拉格朗日乘子：w0,w1,…,wnw0,w1,…,wn， 定义朗格朗日函数 L(P,w):

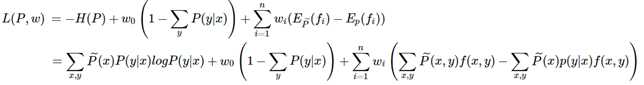
最后得到使得H(P)最大的条件分布P(Y/X)的解：

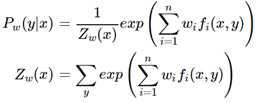
这里 f_i(x,y)代表特征函数，wi代表特征函数的权值， P_w(y|x)即为 MaxEnt 模型，现在内部的极小化求解得到关于w的函数，现在求其对偶问题的外部极大化即可，将最优解记做 w?:

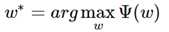
所以现在最大上模型转为求解 Ψ(w)的极大化问题，求解最优的 w?后，便得到了所要求的MaxEnt 模型，将 Pw(y|x)带入 Ψ(w)，最终通过一系列极其复杂的运算，得到了需要极大化的式子：

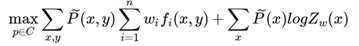
使用极大似然法求解：

这里有训练数据得到经验分布 P?(x,y)， 待求解的概率模型 P(Y|X)的似然函数为：

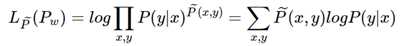
将 P_w(y|x)带入以上公式可以得到：

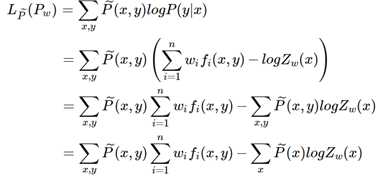
显而易见，拉格朗日对偶得到的结果与极大似然得到的结果是等价的（但并不意味着最大熵模型与最大似然估计等价），现在只需极大化似然函数即可，顺带优化目标中可以加入正则项，这是一个凸优化问题，一般的梯度法、牛顿法都可解之，专门的算法有GIS IIS 算法。

最大熵模型

标签：nbsp   特征   拉格朗日对偶   算法   bsp   条件   假设   外部   目标   

原文地址：https://www.cnblogs.com/yongfuxue/p/10094788.html