标签:ESS 合并 tar 函数的参数 ssi 随机 one default 防止
Gradient Tree Boosting 梯度树提升GTB,又叫做gradient boosting regression tree梯度提升回归树GBRT,有叫做gradient boosting decision tree梯度提升回归树GBDT
GBDT 的优点:
GBDT 的缺点:
GBDT是基于回归树的,回归树和分类树类似,只是在每个树节点都去计算这个节点上所有的树的平均值,分枝时要穷举节点上所有的值,作为阈值进行划分,大于这个值得作为一类,小于这个值的作为一类,计算两部分的均值,并计算方差。方差最小的所对应的阈值作为划分特征。
GD即Gradient Boost,训练一个回归树,计算终节点的平均值,与真实值做对比,将差值输入另外一个回归树,训练这个回归树,将这个回归书的预测值与残差值比较,再把残差值输入另外一个回归树训练,直到最后一个回归树的预测值和输入的残差值相等,也就是所将每个回归树的预测值加起来后等于真实值。
给定输入向量x和输出变量y组成的若干训练样本(x1,y1),(x2,y2),…,(xn,yn),目标是找到近似函数F(x),使得损失函数L(y,F(x))的损失值最小。
L(y,F(x))的典型定义为
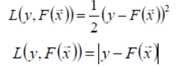
假定最优函数为:
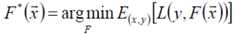
假定F(x)是一族基函数fi(x)的加权和
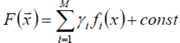
梯度提升方法寻找最优解F(x),使得损失函
数在训练集上的期望最小。方法如下:
首先,给定常函数F0(x):
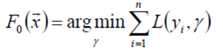
以贪心的思路扩展得到Fm(x):
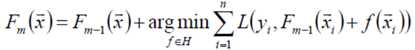
梯度近似:
贪心法在每次选择最优基函数f时仍然困难,使用梯度下降的方法近似计算
将样本带入基函数f得到f(x1),f(x2),...,f(xn),从而L退化为向量L(y1,f(x1)),L(y2,f(x2)),...,L(yn,f(xn))
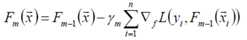
上式中的权值γ为梯度下降的步长,使用线性搜索求最优步长:
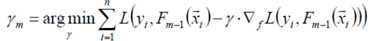
提升算法
初始给定模型为常数
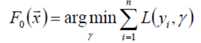
对于m=1到M,计算伪残差
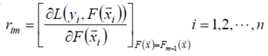
使用数据 计算拟合残差的基函数f m (x)
计算步长,一维优化
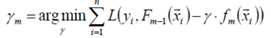
更新模型
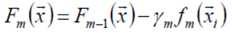
梯度提升决策树GBDT
梯度提升的典型基函数即决策树(尤其是CART),在第m步的梯度提升是根据伪残差数据计算决策树tm(x)。令树tm(x)的叶节点数目为J,即树tm(x)将输入空间划分为J个不相交区域R1m,R2m,...,RJm,并且决策树tm(x)可以在每个区域中给出某个类型的确定性预测。使用指示记号I(x)
使用线性搜索计算学习率,最小化损失函数
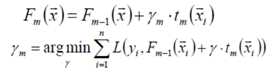
进一步:对树的每个区域分别计算步长,从而系数b jm 被合并到步长中,从而:
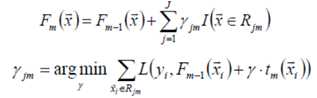
1)叶结点数目控制了树的层数,一般选择4≤J≤8
2)叶结点包含的最少样本数目,防止出现过小的叶结点,降低预测方差
3)梯度提升迭代次数M:增加M可降低训练集的损失值,但有过拟合风险
4)衰减因子、降采样
衰减Shrinkage,又称为学习率v,ν=1即为原始模型;推荐选择v<0.1的小学习率。过小的学习率会造成计算次数增多。
5)降采样
使用随机梯度提升Stochastic gradient boosting:每次迭代都对伪残差样本采用无放回的降采样,用部分样本训练基函数的参数。令训练样本数占所有伪残差样本的比例为f;f=1即为原始模型:推荐0.5≤f≤0.8。
较小的f能够增强随机性,防止过拟合,并且收敛的快。
降采样的额外好处是能够使用剩余样本做模型验证。
1)函数估计本来被认为是在函数空间而非参数空间的数值优化问题,而阶段性的加性扩展和梯度下降手段将函数估计转换成参数估计。
2)损失函数是最小平方误差、绝对值误差等,则为回归问题;而误差函数换成多类别Logistic似然函数,则成为分类问题。
3)对目标函数分解成若干基函数的加权和,是常见的技术手段:神经网络、径向基函数、傅立叶/小波变换、SVM都可以看到它的影子。
1) 分类
from sklearn.ensemble import GradientBoostingClassifier
GradientBoostingClassifier(loss=‘deviance‘, learning_rate=0.1, n_estimators=100, subsample=1.0, criterion=‘friedman_mse‘, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3, min_impurity_decrease=0.0, min_impurity_split=None, init=None, random_state=None, max_features=None, verbose=0, max_leaf_nodes=None, warm_start=False, presort=‘auto‘)
弱学习器(例如:回归树)的数量由参数 n_estimators 来控制;每个树的大小可以通过由参数 max_depth 设置树的深度,或者由参数 max_leaf_nodes 设置叶子节点数目来控制。 learning_rate 是一个在 (0,1] 之间的超参数,这个参数通过 shrinkage(缩减步长) 来控制过拟合。
Note:
超过两类的分类问题需要在每一次迭代时推导 n_classes 个回归树。因此,所有的需要推导的树数量等于n_classes * n_estimators 。对于拥有大量类别的数据集我们强烈推荐使用 RandomForestClassifier 来代替
2) 回归
from sklearn.ensemble import GradientBoostingRegressor
GradientBoostingRegressor(loss=‘ls‘, learning_rate=0.1, n_estimators=100, subsample=1.0, criterion=‘friedman_mse‘, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3, min_impurity_decrease=0.0, min_impurity_split=None, init=None, random_state=None, max_features=None, alpha=0.9, verbose=0, max_leaf_nodes=None, warm_start=False, presort=‘auto‘)
对于回归问题 GradientBoostingRegressor 支持一系列 different loss functions ,这些损失函数可以通过参数 loss 来指定;对于回归问题默认的损失函数是最小二乘损失函数( ‘ls‘ )。可选的loss : {‘ls’, ‘lad’, ‘huber’, ‘quantile’}, optional (default=’ls’)
标签:ESS 合并 tar 函数的参数 ssi 随机 one default 防止
原文地址:https://www.cnblogs.com/yongfuxue/p/10094721.html