标签：数据   概率   数学   期望   思路   def   .com   相同   hdu2897   

几个符号的认识：

• 或      |   ，   c=a|b，二进制下c的第i位为1，当且当a和b的第i位不同时为0，即至少有一个1。
• 异或  ^   ，   c=a^b，二进制下c的第i位为1，当且当a和b的第i位不相同。
• 且     &   ，   c=a|b，二进制下c的第i位为1，当且当a和b的第i位同时为1。

性质：

• ‘或’具有扩散性，即一个数列，‘或’的个数越多，结果越大。
• ‘且’具有收敛性，个数越多，结果越小。

例题： Interview ，CodeForces - 631A

题意：给出两个长度都为N的数组a[] ，b[]，(N<=1000)，让你求最大的F(L,R)；F(L,R)=a[L]|a[L+1]|....a[R]+b[L]|b[L+1]|....|b[R]，即两个区间对应的或运算之和。

思路：数据比较小，那么我们预处理区间或运算结果，复杂度为O(N^2)，然后枚举每个区间，更新答案即可。

如果N<=1e6呢？  我们需要O(N)去做。显然答案是F(1,N)，因为或运算的扩散性！

（引申一下，gcd具有收敛性！

上面与这节课无关，正课：

1，欧拉函数：

什么是欧拉函数：

如何求欧拉函数：

欧拉函数的公式：

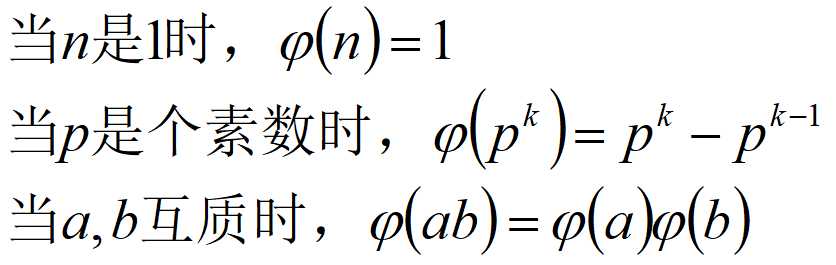
 由上面的公式，联系之前学过的欧拉素数筛法，我们可以O(N)的求出[1,N]的欧拉函数。

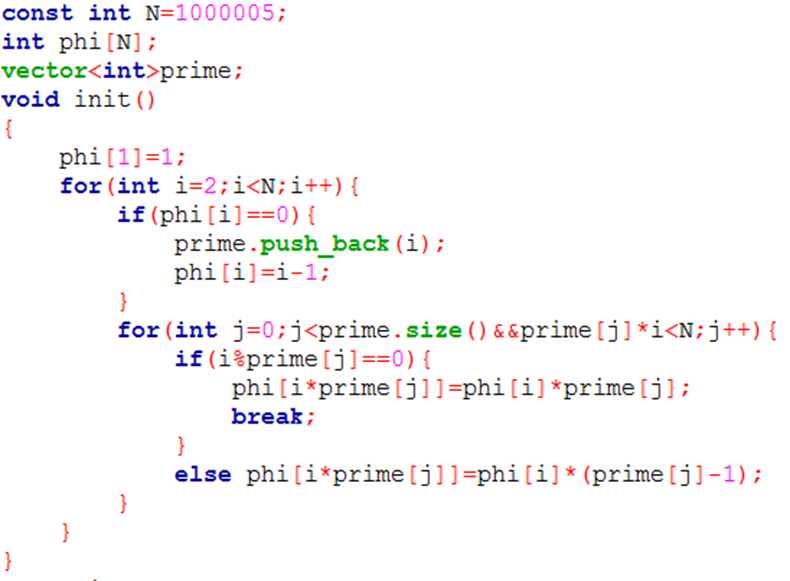
欧拉函数的应用：

1，求逆元。

2，欧拉降幂。

我们知道a^x%p，可以用快速幂来求，复杂度为O(logx)，但是有的时候x过大，这个复杂度也应付不了。久可以用上面的公式，把x减小，再快速幂。

3，累加。有的时候我们可以把一个问题转化为求与x互质的个数有多少，这样就可以用欧拉函数，效率提高。

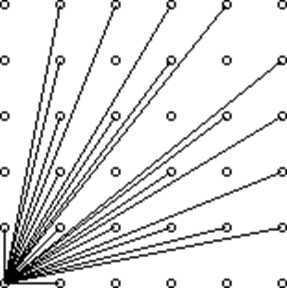
例题：Visible Lattice Points POJ - 3090

题意：给定如果N*N的网格，问在(0,0)可以看到多少个点。N<=1000;

思路：单独考虑(0,0) (0,1) (1,0)；  其他点为(x,y)，这些点一定满足gcd(x,y)==1；比如(4,2)不能被看到，因为它被(2,1)挡住了。

那么我们考虑x>y，那么x一定时，y的个数就是phi[x]，此时贡献为phi[1]+phi[2]+...phi[N]。

那么答案就是3+(phi[1]+phi[2]+...phi[N])*2；  我们预处理出phi的前缀和即可。

2，数学期望

通俗地理解，数学期望就是概率。

这类问题的形式一般如下：

• 给定骰(tou)子，问第一次x正面朝上的期望的多少。
• 给定地图，问玩家从a点到b点的期望的多少。

此类题大部分都是列方程，然后递推。

例题：Coupons UVA - 10288

题意：有N种硬币，给次得到每种硬币的概率相同，问得到N种硬币的期望的多少。

思路：我们用dp[x]表示已经得到了x种硬币的前提下，得到N种硬币的期望。

那么 dp[N]=0;

        dp[x]=dp[x+1]*(1-1/x)+dp[x]*1/x; (x<N)

化简就是dp[x]=(N-x)/N，最后得到dp[0]=N*(1/1+1/2+1/3...+1/N);

更多的数学期望题目可以点击：https://www.cnblogs.com/hua-dong/p/8166093.html

3：博弈

这类题型往往是如下形式：

• 给出一种规则，玩家A和玩家B都用最优的策略，问玩家A是否必胜。
• 如果玩家A必胜，第一步应该怎么玩。

....

最简单的巴什博奕（Bash Game）：

只有一堆N个物品，两个人轮流从这堆物品中取物，规 定每次至少取一个，最多取m个。最后取光者得胜。

当N%(m+1)==0时先手必败，其他情况下必胜。

我们可以类推，N=[1,M]必胜，  N=M+1，先手怎么取都去不完，而对方可以去完，先手必输。

                         N>M+1时，如果N%(M+1)!=0，那么先手取x，使得(N-x)%(M+!)==0即可保证先手能走到M+1这一步，保证了必胜。

例题：hdu2897

更多博弈可以看：https://www.cnblogs.com/hua-dong/p/8397622.html

数学第二课

标签：数据   概率   数学   期望   思路   def   .com   相同   hdu2897   

原文地址：https://www.cnblogs.com/hua-dong/p/10102037.html