标签:open space bit namespace 分享 题目 image code nbsp
题目大意:
https://nanti.jisuanke.com/t/34142
有一个弯道抽象成圆的一部分 车子抽象成矩形
漂移过程中矩形上边会与圆的圆心在同一条直线上
以右上点贴着弯道边缘进行漂移
看不懂题意导致几何题没能做出来 我这个替补选手的临时补位真是愧对队友
所幸是模拟赛 英语渣的痛希望四级放过我
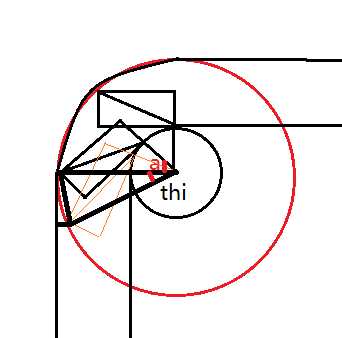
车子漂移时 实际上最远点会画出一个圆 如上红圆
那么当角度为如上a角时 轨道宽度此时必须最大
而角度大于a角时 轨道宽度同样必须为最大 根据勾股定理此时 maxw=sqrt( (a+r)*(a+r)+b*b ) - r
所以此时还需要解决角度小于a时的情况 如上橙色矩形
此时w可小于最大 发现其最远点与等于a角时的最远点 实际上在红圆上形成了一个圆心角 thi
那么就可以计算出thi对应的弦的长度L 而弦与直轨道的夹角ang也是可求的
所以可以得到w的减小值为L*sin(ang) 所以此时 w=maxw-L*sin(ang)
PS: 代码中的角度名与上述讲解并不一一对应

#include <bits/stdc++.h> using namespace std; const double PI=acos(-1.0); const double eps=1e-8; int dcmp(double x) { if(abs(x)<eps) return 0; else return x>0 ? 1:-1; } int main() { int t; scanf("%d",&t); while(t--) { int a,b,r,d; scanf("%d%d%d%d",&a,&b,&r,&d); double maxr=sqrt((a+r)*(a+r)+b*b); double thi=acos((a+r)*1.0/maxr); double arf=d*1.0/180.0*PI; if(dcmp(arf-thi)>=0) printf("%.12f\n",maxr-1.0*r); else { double ang=thi-arf; double ang1=(PI-ang)/2.0; double L=cos(ang1)*maxr*2.0; double ang2=PI/2.0-ang1; double bye=sin(ang2)*L; printf("%.12f\n",maxr-1.0*r-bye); } } return 0; }
2018ICPC焦作 D-Keiichi Tsuchiya the Drift King /// 几何
标签:open space bit namespace 分享 题目 image code nbsp
原文地址:https://www.cnblogs.com/zquzjx/p/10104213.html