码迷，mamicode.com
首页 > 其他好文 > 详细

数据结构开发(5)：线性表的链式存储结构

时间：2018-12-13 23:24:18      阅读：237      评论：0      收藏：0      [点我收藏+]

标签：操作   parameter   cout   构造   函数   深度   需求量   复制   编译错误   

0.目录

1.线性表的链式存储结构

2.单链表的具体实现

3.顺序表和单链表的对比分析

4.小结

1.线性表的链式存储结构

顺序存储结构线性表的最大问题是：

  • 插入和删除需要移动大量的元素！如何解决？

链式存储的定义：

  • 为了表示每个数据元素与其直接后继元素之间的逻辑关系；数据元素除了存储本身的信息外，还需要存储其直接后继的信息。

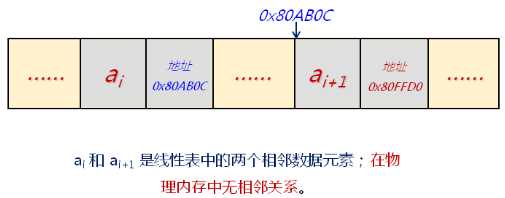
技术分享图片

链式存储逻辑结构：

  • 基于链式存储结构的线性表中，每个结点都包含数据域和指针域
    1. 数据域：存储数据元素本身
    2. 指针域：存储相邻结点的地址

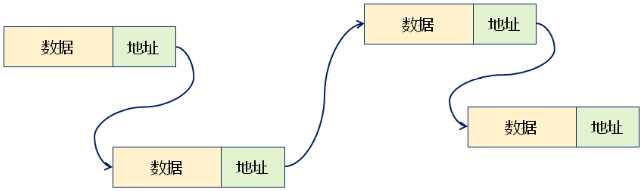
技术分享图片

专业术语的统一：

  • 顺序表
    1. 基于顺序存储结构的线性表
  • 链表
    1. 基于链式存储机构的线性表
      1. 单链表：每个结点只包含直接后继的地址信息
      2. 循环链表：单链表中的最后一个结点的直接后继为第一个结点
      3. 双向链表：单链表中的结点包含直接前驱和后继的地址信息

链表中的基本概念：

  • 头结点
    1. 链表中的辅助结点，包含指向第一个数据元素的指针
  • 数据结点
    1. 链表中代表数据元素的结点，表现形式为：( 数据元素，地址 )
  • 尾结点
    1. 链表中的最后一个数据结点，包含的地址信息为空

单链表中的结点定义：
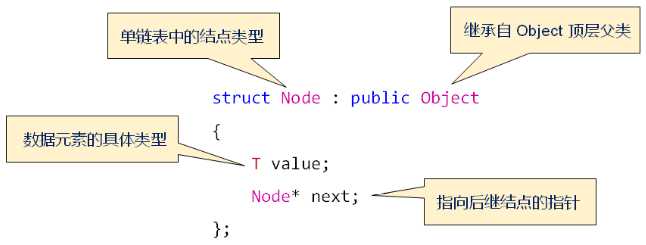
技术分享图片

单链表中的内部结构：
技术分享图片
头结点在单链表中的意义是：辅助数据元素的定位，方便插入和删除操作；因此，头结点不存储实际的数据元素。

在目标位置处插入数据元素：

  1. 从头结点开始，通过current指针定位到目标位置
  2. 从堆空间申请新的Node结点
  3. 执行操作：
    1. node->value = e;
    2. node->next = current->next;
    3. current->next = node;

在目标位置处删除数据元素：

  1. 从头结点开始，通过current指针定位到目标位置
  2. 使用toDel指针指向需要删除的结点
  3. 执行操作：
    1. toDel = current->next;
    2. current->next = toDel->next;
    3. delete toDel;

2.单链表的具体实现

本节目标：

  • 完成链式存储结构线性表的实现

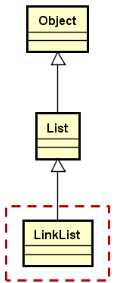
技术分享图片

LinkList 设计要点：

  1. 类模板，通过头结点访问后继结点
  2. 定义内部结点类型Node，用于描述数据域和指针域
  3. 实现线性表的关键操作( 增，删，查，等 )

LinkList的定义：
技术分享图片

链表的实现 LinkList.h：

#ifndef LINKLIST_H
#define LINKLIST_H

#include "List.h"
#include "Exception.h"

namespace StLib
{

template <typename T>
class LinkList : public List<T>
{
protected:
    struct Node : public Object
    {
        T value;
        Node* next;
    };

    mutable Node m_header;
    int m_length;
public:
    LinkList()
    {
        m_header.next = NULL;
        m_length = 0;
    }

    bool insert(const T& e)
    {
        return insert(m_length, e);
    }

    bool insert(int i, const T& e)
    {
        bool ret = ((0 <= i) && (i <= m_length));

        if( ret )
        {
            Node* node = new Node();

            if( node != NULL )
            {
                Node* current = &m_header;

                for(int p=0; p<i; p++)
                {
                    current = current->next;
                }

                node->value = e;
                node->next = current->next;
                current->next = node;

                m_length++;
            }
            else
            {
                THROW_EXCEPTION(NoEnoughMemoryException, "No memory to insert new element ...");
            }
        }

        return ret;
    }

    bool remove(int i)
    {
        bool ret = ((0 <= i) && (i < m_length));

        if( ret )
        {
            Node* current = &m_header;

            for(int p=0; p<i; p++)
            {
                current = current->next;
            }

            Node* toDel = current->next;

            current->next = toDel->next;

            delete toDel;

            m_length--;
        }

        return ret;
    }

    bool set(int i, const T& e)
    {
        bool ret = ((0 <= i) && (i < m_length));

        if( ret )
        {
            Node* current = &m_header;

            for(int p=0; p<i; p++)
            {
                current = current->next;
            }

            current->next->value = e;
        }

        return ret;
    }

    T get(int i) const
    {
        T ret;

        if( get(i, ret) )
        {
            return ret;
        }
        else
        {
            THROW_EXCEPTION(IndexOutOfBoundsException, "Invalid parameter i to get element ...");
        }

        return ret;
    }

    bool get(int i, T& e) const
    {
        bool ret = ((0 <= i) && (i < m_length));

        if( ret )
        {
            Node* current = &m_header;

            for(int p=0; p<i; p++)
            {
                current = current->next;
            }

            e = current->next->value;
        }

        return ret;
    }

    int length() const
    {
        return m_length;
    }

    void clear()
    {
        while ( m_header.next )
        {
            Node* toDel = m_header.next;

            m_header.next = toDel->next;

            delete toDel;
        }

        m_length = 0;
    }

    ~LinkList()
    {
        clear();
    }
};

}

#endif // LINKLIST_H

main.cpp测试

#include <iostream>
#include "LinkList.h"

using namespace std;
using namespace StLib;

int main()
{
    LinkList<int> list;

    for(int i=0; i<5; i++)
    {
        list.insert(0, i);
        list.set(0, i*i);
    }

    for(int i=0; i<list.length(); i++)
    {
        cout << list.get(i) << endl;
    }
    cout << endl;

    list.remove(2);

    for(int i=0; i<list.length(); i++)
    {
        cout << list.get(i) << endl;
    }
    cout << endl;

    list.clear();

    for(int i=0; i<list.length(); i++)
    {
        cout << list.get(i) << endl;
    }

    return 0;
}

运行结果为：

16
9
4
1
0

16
9
1
0

问题：

  • 头结点是否存在隐患？
  • 实现代码是否需要优化？

头结点的隐患：
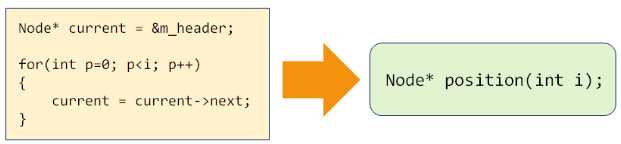
技术分享图片

代码优化：

  • insert，remove，get，set等操作都涉及元素定位。

技术分享图片

代码优化（LinkList.h）：

#ifndef LINKLIST_H
#define LINKLIST_H

#include "List.h"
#include "Exception.h"

namespace StLib
{

template <typename T>
class LinkList : public List<T>
{
protected:
    struct Node : public Object
    {
        T value;
        Node* next;
    };

    mutable struct : public Object
    {
        char reserved[sizeof(T)];
        Node* next;
    } m_header;

    int m_length;

    Node* position(int i) const
    {
        Node* ret = reinterpret_cast<Node*>(&m_header);

        for(int p=0; p<i; p++)
        {
            ret = ret->next;
        }

        return ret;
    }
public:
    LinkList()
    {
        m_header.next = NULL;
        m_length = 0;
    }

    bool insert(const T& e)
    {
        return insert(m_length, e);
    }

    bool insert(int i, const T& e)
    {
        bool ret = ((0 <= i) && (i <= m_length));

        if( ret )
        {
            Node* node = new Node();

            if( node != NULL )
            {
                Node* current = position(i);

                node->value = e;
                node->next = current->next;
                current->next = node;

                m_length++;
            }
            else
            {
                THROW_EXCEPTION(NoEnoughMemoryException, "No memory to insert new element ...");
            }
        }

        return ret;
    }

    bool remove(int i)
    {
        bool ret = ((0 <= i) && (i < m_length));

        if( ret )
        {
            Node* current = position(i);
            Node* toDel = current->next;

            current->next = toDel->next;

            delete toDel;

            m_length--;
        }

        return ret;
    }

    bool set(int i, const T& e)
    {
        bool ret = ((0 <= i) && (i < m_length));

        if( ret )
        {
            position(i)->next->value = e;
        }

        return ret;
    }

    T get(int i) const
    {
        T ret;

        if( get(i, ret) )
        {
            return ret;
        }
        else
        {
            THROW_EXCEPTION(IndexOutOfBoundsException, "Invalid parameter i to get element ...");
        }

        return ret;
    }

    bool get(int i, T& e) const
    {
        bool ret = ((0 <= i) && (i < m_length));

        if( ret )
        {
            e = position(i)->next->value;
        }

        return ret;
    }

    int length() const
    {
        return m_length;
    }

    void clear()
    {
        while ( m_header.next )
        {
            Node* toDel = m_header.next;

            m_header.next = toDel->next;

            delete toDel;
        }

        m_length = 0;
    }

    ~LinkList()
    {
        clear();
    }
};

}

#endif // LINKLIST_H

3.顺序表和单链表的对比分析

问题

  • 如何判断某个数据元素是否存在于线性表中？

遗失的操作——find：

  • 可以为线性表( List )增加一个查找操作
  • int find(const T& e) const;
    1. 参数：
      1. 待查找的数据元素
    2. 返回值：

      1. =0：数据元素在线性表中第一次出现的位置

      2. -1：数据元素不存在

数据元素查找示例：
技术分享图片

实现查找find函数：
在List.h中加入

virtual int find(const T& e) const = 0;

在SeqList.h中加入

    int find(const T& e) const
    {
        int ret = -1;

        for(int i=0; i<m_length; i++)
        {
            if( m_array[i] == e )
            {
                ret = i;
                break;
            }
        }

        return ret;
    }

在LinkList.h中加入

    int find(const T& e) const
    {
        int ret = -1;
        int i = 0;
        Node* node = m_header.next;

        while ( node )
        {
            if( node->value == e )
            {
                ret = i;
                break;
            }
            else
            {
                node = node->next;
                i++;
            }
        }

        return ret;
    }

但是若用类对象来进行测试，会有严重的bug：

#include <iostream>
#include "LinkList.h"

using namespace std;
using namespace StLib;

class Test
{
    int i;
public:
    Test(int v = 0)
    {
        i = v;
    }
};

int main()
{
    Test t1;
    Test t2;
    Test t3;
    LinkList<Test> list;

    return 0;
}

编译错误信息：

error C2678: 二进制“==”: 没有找到接受“Test”类型的左操作数的运算符(或没有可接受的转换)

于是应该在顶层父类Object中实现重载比较操作符
Object.h

    bool operator == (const Object& obj);
    bool operator != (const Object& obj);

Object.cpp

bool Object::operator == (const Object& obj)
{
    return (this == &obj);
}

bool Object::operator != (const Object& obj)
{
    return (this != &obj);
}

main.cpp再测试

#include <iostream>
#include "LinkList.h"

using namespace std;
using namespace StLib;

class Test : public Object
{
    int i;
public:
    Test(int v = 0)
    {
        i = v;
    }

    bool operator == (const Test& t)
    {
        return (i == t.i);
    }
};

int main()
{
    Test t1(1);
    Test t2(2);
    Test t3(3);
    LinkList<Test> list;

    list.insert(t1);
    list.insert(t2);
    list.insert(t3);

    cout << list.find(t2) << endl;

    return 0;
}

运行结果为：

1

时间复杂度对比分析：
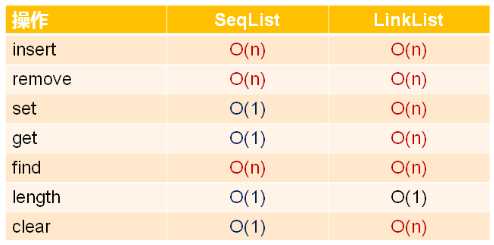
技术分享图片

有趣的问题：

  • 顺序表的整体时间复杂度比单链表要低，那么单链表还有使用价值吗？

效率的深度分析：

  • 实际工程开发中，时间复杂度只是效率的一个参考指标
    1. 对于内置基础类型，顺序表和单链表的下效率不相上
    2. 对于自定义类类型，顺序表在效率上低于单链表
  • 插入和删除
    1. 顺序表：涉及大量数据对象的复制操作
    2. 单链表：只涉及指针操作，效率与数据对象无关
  • 数据访问
    1. 顺序表：随机访问，可直接定位数据对象
    2. 单链表：顺序访问，必须从头访问数据对象，无法直接定位

工程开发中的选择：

  • 顺序表
    1. 数据元素的类型相对简单，不涉及深拷贝
    2. 数据元素相对稳定，访问操作远多于插入和删除操作
  • 单链表
    1. 数据元素的类型相对复杂，复制操作相对耗时
    2. 数据元素不稳定，需要经常插入和删除，访问操作较少

4.小结

  • 链表中的数据元素在物理内存中无相邻关系
  • 链表中的结点都包含数据域和指针域
  • 头结点用于辅助数据元素的定位，方便插入和删除操作
  • 插入和删除操作需要保证链表的完整性
  • 通过类模板实现链表，包含头结点成员和长度成员
  • 定义结点类型，并通过堆中的结点对象构成链式存储
  • 为了避免构造错误的隐患，头结点类型需要重定义
  • 代码优化是编码完成后必不可少的环节
  • 线性表中元素的查找依赖于相等比较操作符( == )
  • 顺序表适用于访问需求量较大的场合( 随机访问 )
  • 单链表适用于数据元素频繁插入删除的场合( 顺序访问 )
  • 当数据类型相对简单时，顺序表和单链表的效率不相上下

数据结构开发(5)：线性表的链式存储结构

标签：操作   parameter   cout   构造   函数   深度   需求量   复制   编译错误   

原文地址：https://www.cnblogs.com/PyLearn/p/10116981.html
踩
(0)
赞
(0)
   
举报
评论 一句话评论（0）
登录后才能评论！
分享档案
更多>
2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)
周排行
mamicode.com排行更多图片
更多
友情链接
兰亭集智   国之画   百度统计   站长统计   阿里云   chrome插件   新版天听网
关于我们 - 联系我们 - 留言反馈
© 2014 mamicode.com 版权所有  联系我们:gaon5@hotmail.com
迷上了代码！