1. 机器学习流程简介

    1）一次性设置（One time setup）
          - 激活函数（Activation functions）

          - 数据预处理（Data Preprocessing）

          - 权重初始化（Weight Initialization）

          - 正则化（Regularization：避免过拟合的一种技术）

          - 梯度检查（Gradient checking）

    2）动态训练（Training dynamics）
          - 跟踪学习过程 （Babysitting the learning process）

          - 参数更新 （Parameter updates)

          - 超级参数优化（Hyperparameter optimization）

          - 批量归一化（BN：Batch Normalization：解决在训练过程中数据分布发生改变的问题，以防止梯度消失或爆炸、加快训练速度）
    3）评估（Evaluation）
          - 模型组合（Model ensembles）

             (训练多个独立的模型，取这些模型结果的平均值)

   神经网络学习过程本质就是为了：学习数据分布，那么网络的泛化能力也大大降低，使训练数据与测试数据的分布相同。

2. 激活函数（Activation Functions）

    详细内容参见：激活函数

    总结：

     1）使用ReLU时     2）尝试使用Leaky ReLU/Maxout/ELU

     3）可以使用tanh     4）不要使用sigmoid

3. 数据预算处理（Data Preprocessing）

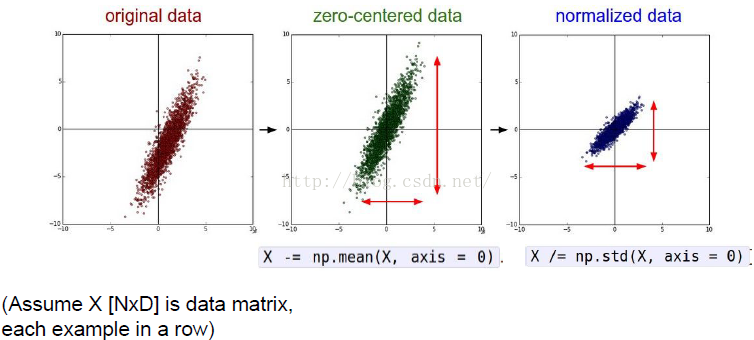
     1）为什么输入数据需要归一化（Normalized Data）？

           归一化后有什么好处呢？原因在于神经网络学习过程本质就是为了学习数据分布，那么网络的泛化能力也大大降低；另外一方面，那么网络就要在每次迭代都去学习适应不同的分布，这也正是为什么我们需要对数据都要做一个归一化预处理的原因。

          对于深度网络的训练是一个复杂的过程，那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变，所以如果训练过程中，那么将会影响网络的训练速度。

4. 权重初始化（Weight Initialization）

    1）小的随机数

         w= 0.01 * np.random.randn(fan_in    2）神经元将饱和         w = 1.0 * np.random.randn(fan_in    3）合理的初始化（Xavier init）

         w = np.random.randn((fan_in    权重初始化是一个重要的研究领域。

5. 批量归一化（BN: Batch Normalization)

5.1 BN训练    

    1）随机梯度下降法（SGD）对于训练深度网络简单高效，就是需要我们人为的去选择参数，以至于我们很多时间都浪费在这些的调参上。那么使用BN（详见论文《Batch Normalization_ Accelerating Deep Network Training by Reducing Internal Covariate Shift》）之后可以不需要那么刻意的慢慢调整参数。

    2）神经网络一旦训练起来，除了输入层的数据外(因为输入层数据，后面网络每一层的输入数据分布是一直在发生变化的，前面层训练参数的更新将导致后面层输入数据分布的变化。以网络第二层为例：网络的第二层输入，而第一层的参数在整个训练过程中一直在变化，数据分布的改变称之为：“Internal  Covariate Shift”。Paper所提出的算法，中间层数据分布发生改变的情况，这个牛逼算法的诞生。

   3）BN的地位：与激活函数层、卷积层、全连接层、池化层一样   4）BN的本质原理：在网络的每一层输入的时候，也就是先做一个归一化处理（归一化至：均值0、方差为1），可不像我们想象的那么简单一个可学习、有参数（γ、β）的网络层。

   5）归一化公式：

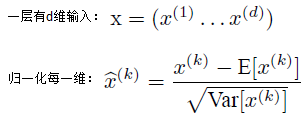
   6）如果是仅仅使用上面的归一化公式，然后送入网络下一层B，你强制把它给我归一化处理、标准差也限制在了1，这样就相当于我这一层网络所学习到的特征分布被你搞坏了，引入了可学习参数γ、β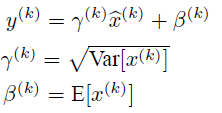       

       上面的公式表明参数γ、β是可以恢复出原始的某一层所学到的特征的。

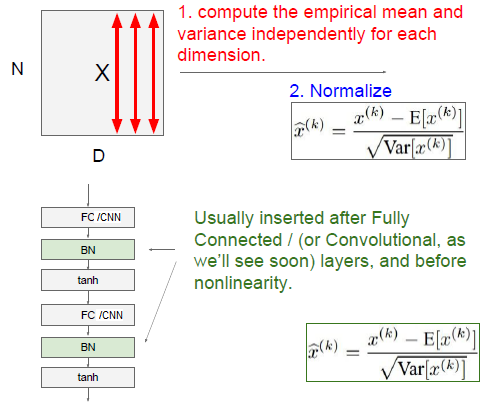
     7）引入了这个可学习重构参数γ、β             

     8）BN层是对于每个神经元做归一化处理，而不是对一整层网络的神经元进行归一化。既然BN是对单个神经元的运算，每个特征图的大小是100*100，如果采用BN，这样岂不是太恐怖了。因此卷积层上的BN使用，把一整张特征图当做一个神经元进行处理。

    9）卷积神经网络经过卷积后得到的是一系列的特征图，那么网络某一层输入数据可以表示为四维矩阵(m,w，m为min-batch sizes，w、h分别为特征图的宽高。在CNN中我们可以把每个特征图看成是一个特征处理（一个神经元），mini-batch size 的大小就是：m*w*h，这就是相当于求取所有样本所对应的一个特征图的所有神经元的平均值、方差    10)    在使用BN前减小学习率、小心的权重初始化的目的是：使其输出的数据分布不要发生太大的变化。

    11） BN的作用：

       1）改善流经网络的梯度

       2）允许更大的学习率大幅提高训练速度：

            你可以选择比较大的初始学习率，甚至在网络训练到一半的时候，现在我们可以采用初始很大的学习率，因为这个算法收敛很快。当然这个算法即使你选择了较小的学习率，因为它具有快速训练收敛的特性；

       3）减少对初始化的强烈依赖

       4）改善正则化策略：作为正则化的一种形式            你再也不用去理会过拟合中drop out、L2正则项参数的选择问题，你可以移除这两项了参数，因为BN具有提高网络泛化能力的特性；

       5）再也不需要使用使用局部响应归一化层了（局部响应归一化是Alexnet网络用到的方法，因为BN本身就是一个归一化网络层；

       6）可以把训练数据彻底打乱（防止每批训练的时候，文献说这个可以提高1%的精度）。

       注：以上为学习过程，均值和方差(mean/std)不基于小批量进行计算     

5.2 BN测试

     1）实际测试时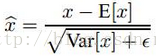         

        这里的均值和方差已经不是针对某一个Batch了，在训练过程中除了正常的前向传播和反向求导之外，以便训练完成之后按照下式计算整体的均值和方差：  

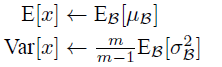
       上面简单理解就是：对于均值来说直接计算所有batch u值的平均值；然后对于标准偏差采用每个batch σB的无偏估计。最后测试阶段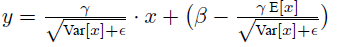        

     2）BN可以应用于一个神经网络的任何神经元上。文献主要是把BN变换，激活函数层是这样的：

                              z=g(Wu+b)

          也就是我们希望一个激活函数，比如s型函数s(x)的自变量x是经过BN处理后的结果。因此前向传导的计算公式就应该是：
                              z=g(BN(Wu+b))

          其实因为偏置参数b经过BN层后其实是没有用的，当然BN层后面还有个β参数作为偏置项                               z=g(BN(Wu))

6. 跟踪训练过程

   1）Learning Rate

         - Learning Rate太小(如1e-6)         - Learning Rate太大(如1e-6)，cost增长爆炸 (cur cost > 3* original cost)

         - 在[1e-3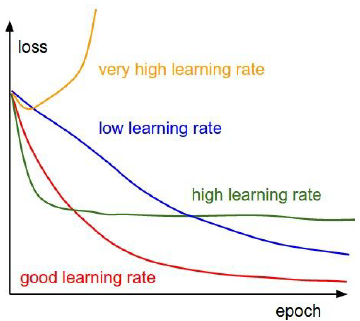       

     2）Mini-batch SGD

           Loop:

           1. Sample a batch of data

           2. Forward prop it through the graph           3. Backprop to calculate the gradients

           4. Update the parameters using gradient

7. 参数优化

    参数优化直观显示图 

    参数优化的目的是：减少损失(loss)    Caffe Solver7.1 Gradient Descent Variants

7.1.1 Batch gradient descent

      

   for i in range(nb_epochs):
     params_grad = evaluate_gradient(loss_function, params)
     params = params - learning_rate * params_grad

7.1.2 SGD(Stochastic Gradient Descent: 随机梯度下降)

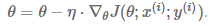
     每次基于一个数据样本计算梯度。

  for i in range(nb_epochs):
    np.random.shuffle(data)
    for example in data:
      params_grad = evaluate_gradient(loss_function, params)
      params = params - learning_rate * params_grad

7.1.3 Mini-batch Gradient Descent

       

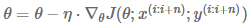
    每次基于n个数据样本计算梯度。

  for i in range(nb_epochs):
    np.random.shuffle(data)
    for batch in get_batches(data, batch, params)
      params = params - learning_rate * params_grad

    1）减少参数更新的变化    2）使用先进的Deep Learning库    注：n一般取[50，视具体应用而定。

7.1.4 梯度下降算法面临的挑战

   1）选择合适的Learning Rate是困难的，太大阻碍收敛或且导致损失函数在最小值附近波动或发散；
   2）预先定义的Learning Rate变动规则不能适应数据集的特性；
   3）同样的Learning Rate运用到所有的参数更新(后面的AdaGrad, RMSProp, Adam为解决此问题而生)；
   4）最小化高度非凸损失函数的羝问题是：避免陷入众多的局部最优值。    

7.2 Momentum（动量）

     关键优点： 利用物体运动时的惯性，且减少振荡。

      关键缺点：球盲目地沿着斜坡向山下滚。

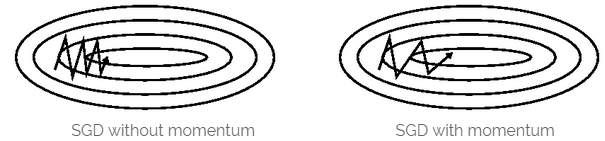
     当Loss function的表面曲线的一维比其它维有更多的沟壑时，如上图左边所示，然后犹犹豫豫地向局部最优点前进。

     Momentum即动量，即更新的时候在一定程度上保留之前更新的方向，可以在一定程度上增加稳定性，并且还有一定摆脱局部最优的能力： 

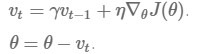
    # Momentum update
    V = gama * V + learning_rate * dw  # integrate velocity
    w -= V                             # integrate position

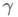     就是Momentum，0.9，有时随着时间而变化表示要在多大程度上保留原来的更新方向，在训练开始时，所以初始值一般选为0.5；当梯度不那么大时，即当前batch的梯度多大程度上影响最终更新方向与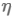之和不一定为1。

     Momentum的物理解释是：当我们把球推下山时，速度越来越快（直到其最大速度,如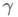<1），梯度方向不停变化的维度的动量不停地减少更快的收敛速度并减少振荡。

7.3 Nesterov Accelerated Gradient (NAG)

      关键优点：一个聪明的球，且知道在斜坡向上之前减速。

                        沿着当前方向，然后再看向哪个方向走最快，可以做出明智的决策。

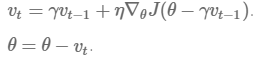
   w_ahead = w - gama * v
   # evaluate dw_ahead (the gradient at w_ahead instead of at w)
   v = gama * v + learning_rate * dw_ahead
   w -= v

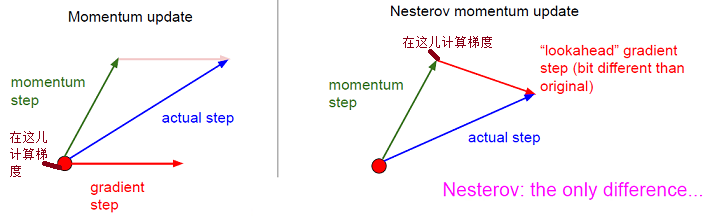
       Momentum：

            1）计算当前的梯度（上图中：比较小的蓝色向量）

            2）沿着更新的累积的梯度方向进行一大跳（上图中：比较大的蓝色向量）

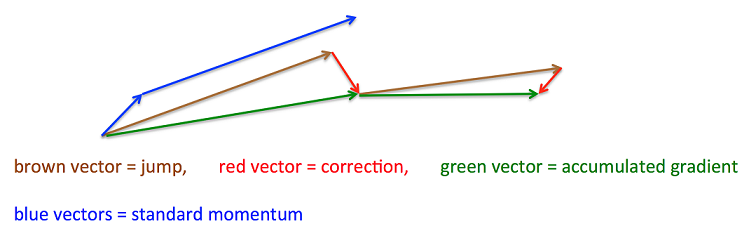
       NAG：

            1）沿着以前累积的梯度方向进行一大跳 （上图中：棕色向量）

            2）在新的位置测量梯度            3）这个有预料的更新可以防止走的太快并导致增加的响应

       关键区别：

            1）计算梯度的位置不一样

7.4 每个参数有自适应的学习率(Per-parameter Adaptive Learning Rate)

      本章描述的方法（AdaGrad、AdaDelta、RMSprop、Adam）专为解决Learning Rate自适应的问题。

      前面讨论的基于梯度的优化方法（SGD、Momentum、NAG）的Learning Rate是全局的      参数的有些维度变化快，有些维度是正的斜坡（如鞍点）；采用相同的Learning Rate是不科学的比如有的参数可能已经到了仅需要微调的阶段，还需要较大幅度的调动。理想的方案是根据参数每个维度的变化率      下面讨论如何自适应Learing Rate的方案：AdaGrad、AdaDelta、RMSProp、Adam。

7.4.1 AdaGrad（Adaptive Gradient ）

     AdaGrad方法给参数的每个维度给出适应的Learning Rate。给不经常更新的参数以较大的Learning Rate     在AdaGrad中     其公式如下：

    
θi

     其示意代码如下：

# Assume the gradient dx and parameter vector x
cache += dx**2
x -= learning_rate * dx / (np.sqrt(cache + 1e-8))

     learning_rate 是初始学习率，所以初始值就不像之前的算法那样重要了。而1e-8指一个比较小的数     其含义是，随着其更新的总距离增多7.4.2 AdaDelta (Adaptive Delta)

    关键优点：1) 解决了AdaGrad Learning Rate单调递减的问题。 (是AdaGrad的扩展)

                      2) 不需要设置默认的Learning Rate 

   RMS(Root Mean Squared) : 均方根

   Adagrad算法存在三个问题：

7.4.3 RMSprop

     RMSprop是由Geoff Hinton设计的。RMSprop与AdaDelta的目的一样：解决AdaGrad的Learning Rate逐步消失的问题。

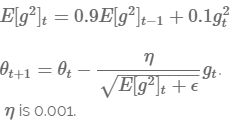
7.4.4 Adam (Adaptive Moment Estimation)

    Adam的目的是：为每个参数计算自适应的Learning Rate。

     其实际效果与AdaDelta、RMSProp相比7.5 优化算法效果可视化

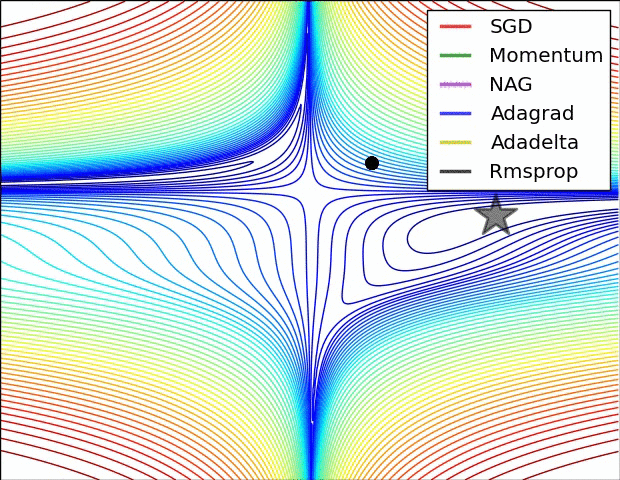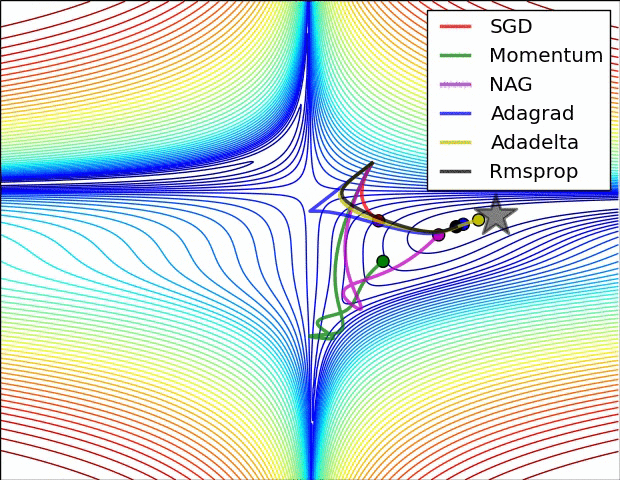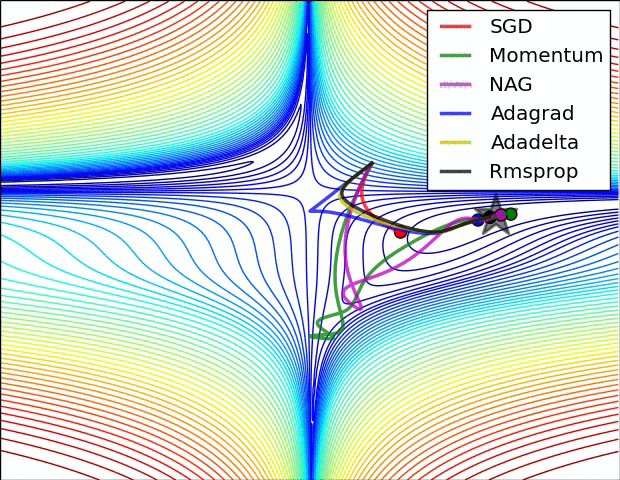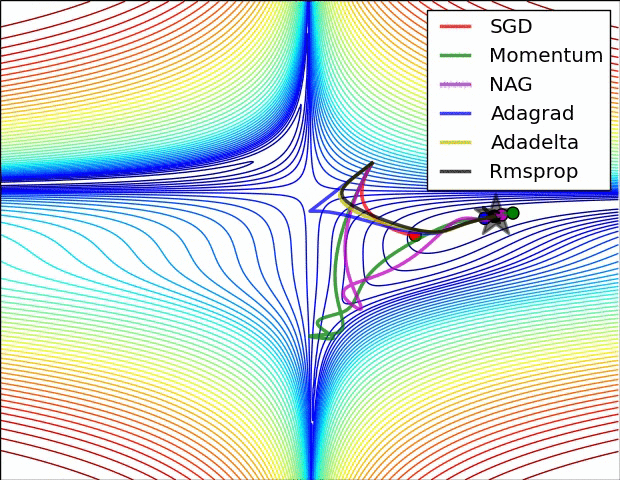
              SGD optimization on Beale‘s function

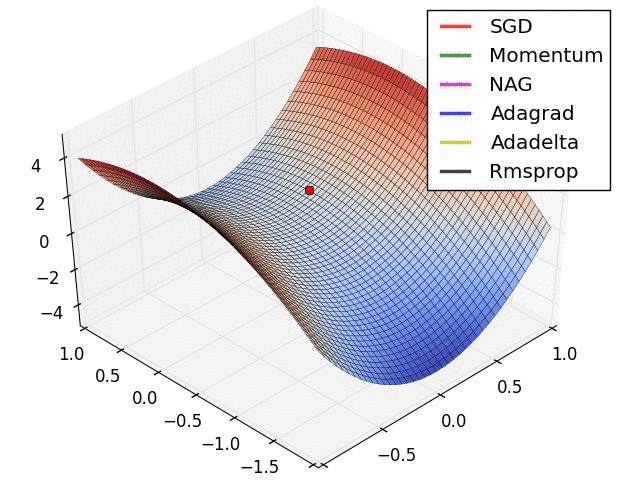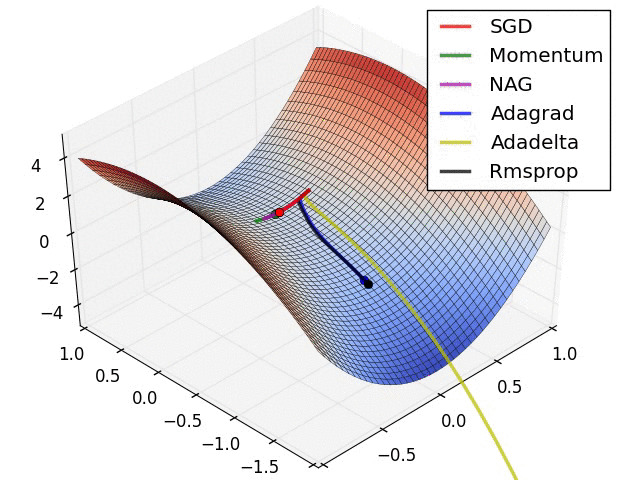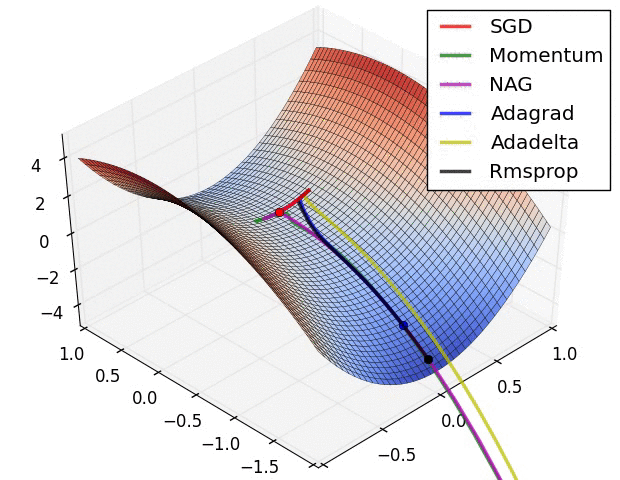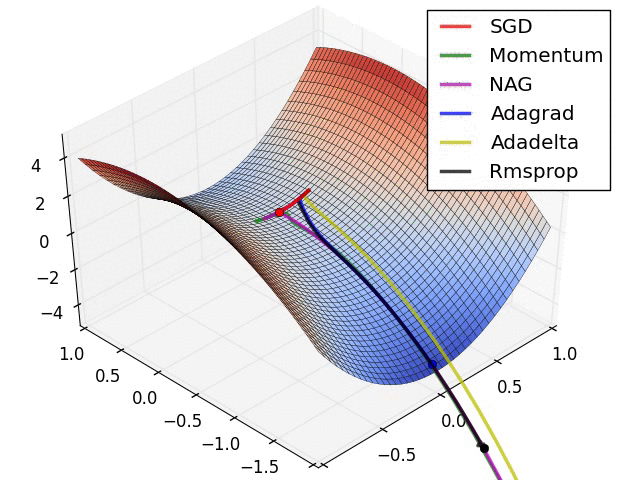
                SGD optimization on Long Valley

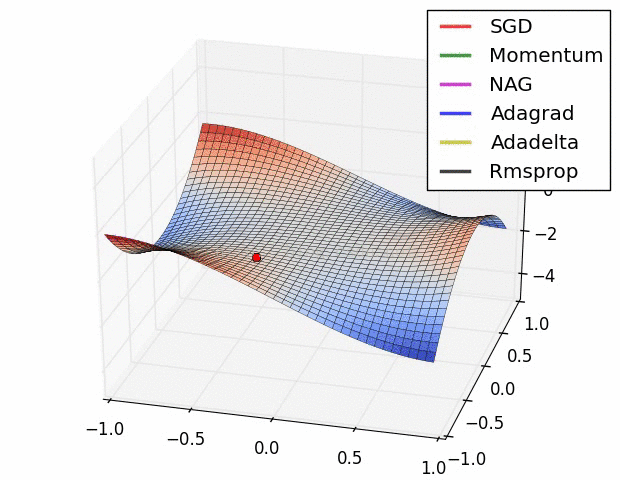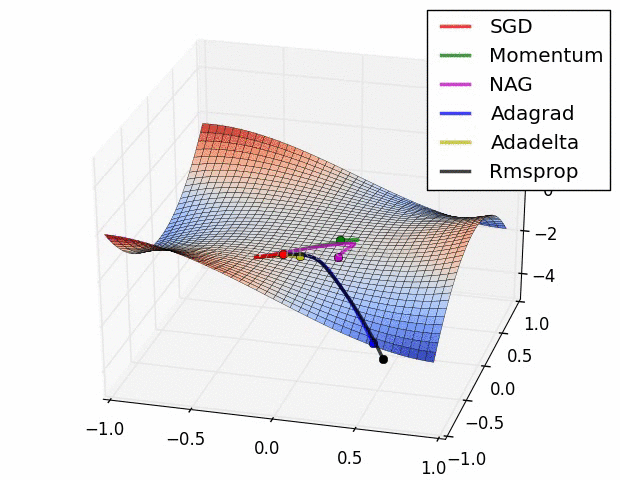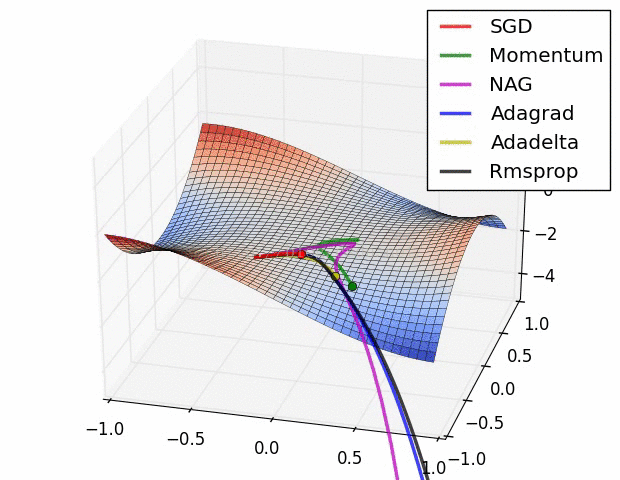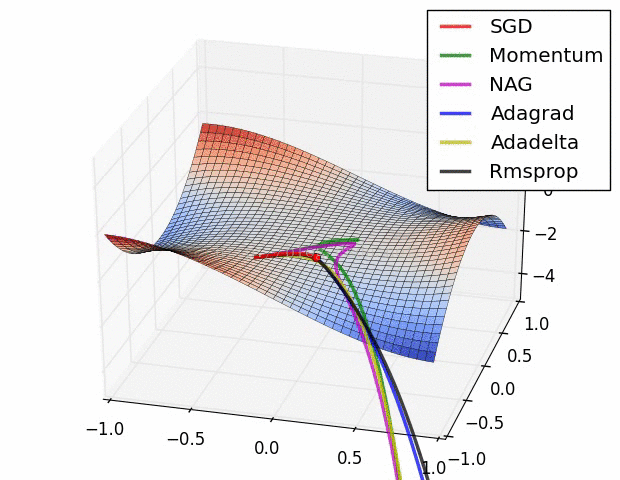
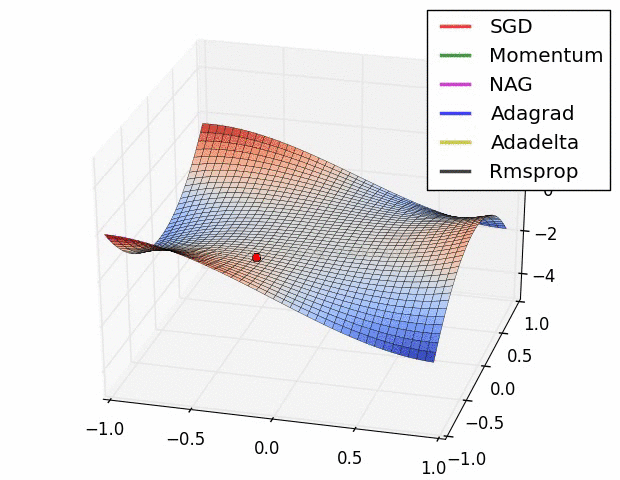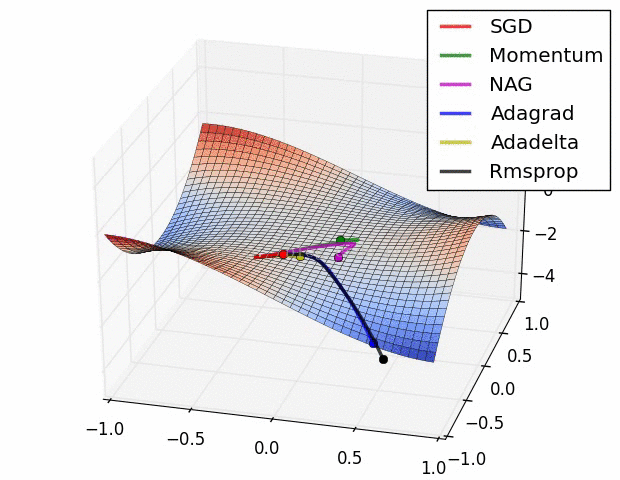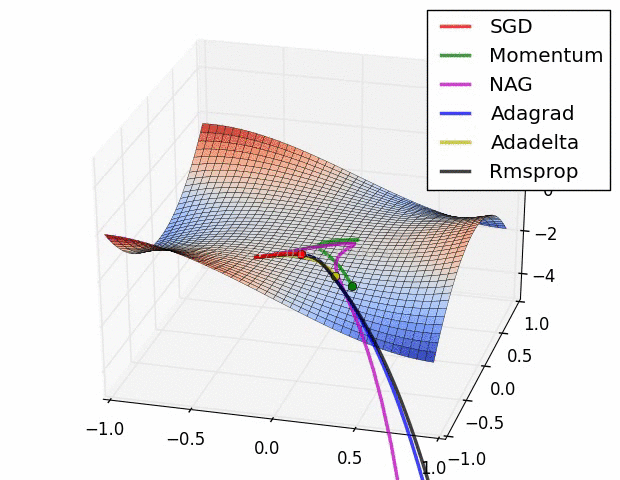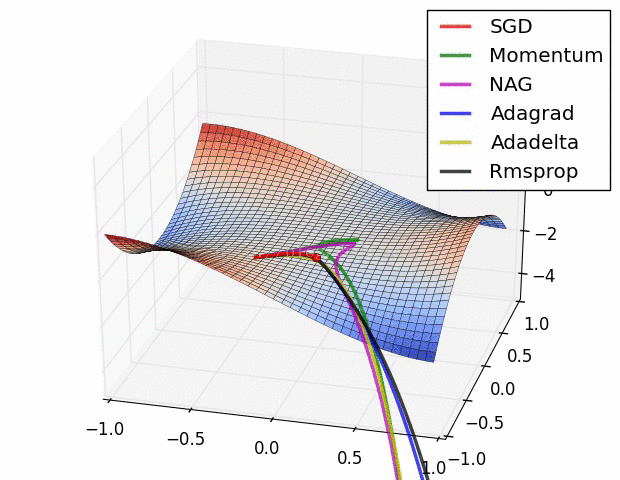
                SGD optimization on Saddle Point

7.6 如何选择优化算法

     1）总结：

           - RMSprop是AdaGrad的扩展           - RMSprop与AdaDelta相比，其它相同

           - Adam与RMSprop相比           - RMSprop、AdaDelta和Adam是非常类似的算法，效果相当

7.7 优化SGD的其它策略

7.7.1 Shuffling and Curriculum Learning

      1）Shuffling：每次迭代前      2）Curriculum Learning：把训练样本按某种有意义的方式进行排序7.7.2 批量归一化Batch Normalization （BN）        

      为了便于训练，通过mean=0，我们不同程度地更新参数，这将降低训练速度且放大变化      BN为每一个mini-batch重建归一化参数。使模型结构的部分进行归一化，且参数初始化要求没哪么高。

      此外作为一个正则化（Regularizer)      正则化（Regularizer)：是一个用于解决过拟合(Overfitting)问题的一种技术。具体实现方法是在损失函数中增加惩罚因子（参数向量的范数7.7.3 早期停止（Early Stopping）

     在训练时，如果验证集的错误率不能得到改善8. Regularization: Dropout

    在前向计算时，如下图所示：

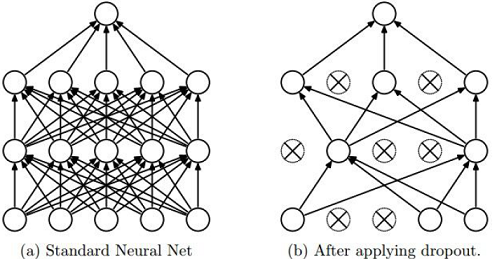
    示意代码如下：

 　　 p = 0.5  # probability of keeping a unit active, np.dot(W1, X) + b1)
      M1 = np.random.rand(*H1.shape) < p  # first dropout mask
      H1 *= M1   # drop

      H2 = np.maximum(0, H1) + b2)
      M2 = np.random.rand(*H2.shape) < p  # send dropout mask
      H2 *= M2   # drop 
      out = np.dot(W3，一个dropout mask对应一个模型    

在测试时， 直接计算每层的激活值，其代码如下：

   def predict(X):
      # ensembled forward pass
      H1 = np.maxmium(0,X)+b1) * p  # Note: scale the activations
      H2 = np.maxmium(0,H1)+b2) * p # Note: scale the activations
      out = np.dot(W3,H2) + b3