标签:根据 获得 math bubuko 随机选择 rsa算法 方法 直接 limit
针对马尔科夫模型不完全已知,即转移概率未知,不能全概率展开的情况,上一篇介绍了策略评估的方法,这一篇对应介绍策略改进的方法,分别是
针对每一个完整决策过程,先估计策略再改进策略的蒙特卡洛同策略学习方式;
针对完整决策过程中的每一步状态动作对生成,评估改进同一个策略$\pi$的时序差分同策略Sarsa学习方式;
针对完整决策过程中的每一步状态动作对生成,评估策略$\pi$过程中利用未来最大化的贪心策略$\beta$的时序差分异策略Q-learning学习方式。
像动态规划里解释的一样,迭代收敛得到了新的$v_\pi$后,就可以依据新的$v_\pi$改进我们的策略$\pi$。改进的策略$\pi$又可以继续迭代收敛到新的$v_\pi$,如此循环,最终收敛至$\pi^*$,
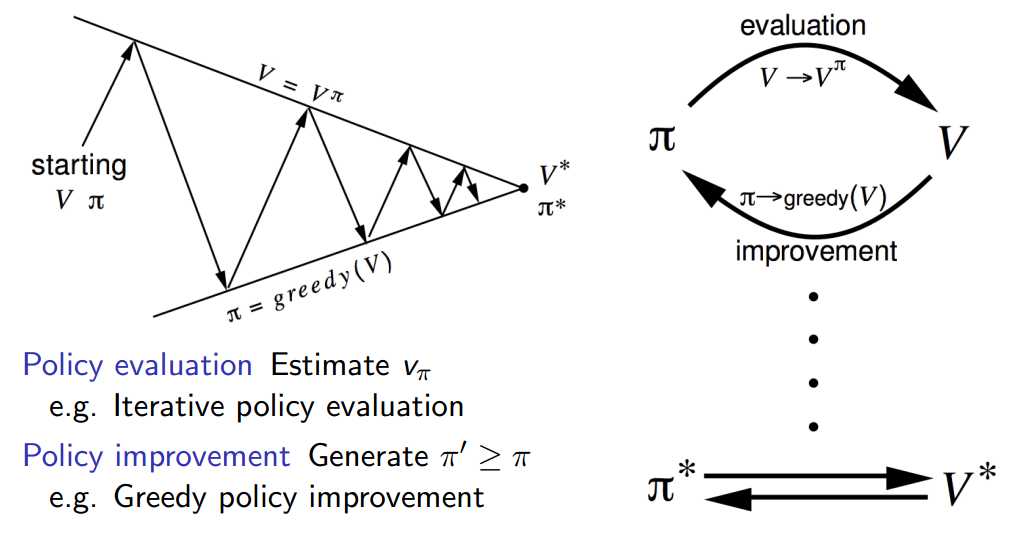
但是我们没有办法像动态规划里一样,直接贪心选择最优的策略$\pi$,因为此时的马尔科夫模型是部分已知的,不能全概率展开来求得最优。所以我们利用$\varepsilon {\rm{ - Greedy}}$算法,
\[\pi \left( {a|s} \right) = \left\{ \begin{array}{l}
\varepsilon /m + 1 - \varepsilon \\
\varepsilon /m
\end{array} \right.\begin{array}{*{20}{c}}
{{\rm{ if }}a* = \mathop {\arg \max }\limits_{a \in A} Q(s,a)}\\
{{\rm{otherwise}}}
\end{array}\]
以$\varepsilon$的概率探索,随机选择动作,来得到奖励反馈,从而更新Q值;以$1-\varepsilon$的概率利用,选择目前Q值最大的动作,来保证整体奖励尽可能大。
所以蒙特卡洛学习过程如下,
初始化Q表,
1. 基于现有的Q表,利用$\varepsilon {\rm{ - Greedy}}$策略$\pi$(以$\varepsilon$的概率随机探索,从而丰富Q表的估计;以$1-\varepsilon$的概率选择目前Q值最大的动作,以获得最大奖励),从$s_0$开始生成一个完整的episode,也就是许多个状态-动作对$(s,a) $;
2. 对该episode中的每一个状态-动作对$(s,a) $:
计算平均累积奖励$G(s,a) $
更新Q值,${Q_\pi }(s,a) \leftarrow {Q_\pi }(s,a) + \alpha (G(s,a) - {Q_\pi }(s,a))$;
3. 依据新的Q表,更新新的策略$\pi$;
4. 重复以上步骤,从许多个episode中不断更新Q表,从而获得最优策略$\pi*$。
像动态规划里解释的一样,为了加快收敛速度,我们可以在$v_\pi$还没有收敛的迭代过程中,就立马改进$v$,利用这个更新的$v$,立马对应更新策略$\pi$,再循环这个过程。注意我们为了使策略生成状态-动作对的过程保持一定的探索率,同样利用$\varepsilon {\rm{ - Greedy}}$策略$\pi$。
!!!
在更新$Q$的过程中,我们有两种方式,第一种是同策略的Sarsa,第二种是异策略的Q-learning。
就是计算下一个状态动作值函数Q时,是仍利用我们评估的$\varepsilon {\rm{ - Greedy}}$策略$\pi$(同策略),还是直接利用贪心策略最大值$Greedy$策略$\beta$。
\[\begin{array}{l}
{Q_\pi }(s,a) \leftarrow {Q_\pi }(s,a) + \alpha (R + \gamma {Q_\pi }(s‘,a‘) - {Q_\pi }(s,a))\\
{Q_\pi }(s,a) \leftarrow {Q_\pi }(s,a) + \alpha (R + \gamma {\max _a}Q(s‘,a) - {Q_\pi }(s,a))
\end{array}\]
!!!
Sarsa算法过程如下,
初始化Q表,
对每一个episode:
从$s_0$开始,对episode中的每一步:
利用$\varepsilon {\rm{ - Greedy}}$策略$\pi$,根据当前状态$s$选择动作$a$,得到奖励$r$,下一时刻状态$s‘$;
仍根据当前Q值对应的$\varepsilon {\rm{ - Greedy}}$策略$\pi$,根据下一状态$s‘$选择动作$a‘$,计算下一时刻的${Q_\pi }(s‘,a‘)$
利用已经得到的奖励$r$和计算得到的下一时刻的${Q_\pi }(s‘,a‘)$,更新现在的${Q_\pi }(s,a)$,${Q_\pi }(s,a) \leftarrow {Q_\pi }(s,a) + \alpha (R + \gamma {Q_\pi }(s‘,a‘) - {Q_\pi }(s,a))$;
重复上述步骤至episode结束。
重复以上步骤,从许多个episode中的每一步中不断学习,从而获得最优策略$\pi*$。
Q-learning算法过程如下,
初始化Q表,
对每一个episode:
从$s_0$开始,对episode中的每一步:
利用$\varepsilon {\rm{ - Greedy}}$策略$\pi$,根据当前状态$s$选择动作$a$,得到奖励$r$,下一时刻状态$s‘$;
利用已经得到的奖励$r$和基于现有Q表下一状态的最大可能取值${\max _a}Q(s‘,a)$,更新现在的${Q_\pi }(s,a)$,${Q_\pi }(s,a) \leftarrow {Q_\pi }(s,a) + \alpha (R + \gamma {\max _a}Q(s‘,a) - {Q_\pi }(s,a))$;
重复上述步骤至episode结束。
重复以上步骤,从许多个episode中的每一步中不断学习,从而获得最优策略$\pi*$。
4. 免模型策略改进——蒙特卡洛(Monte-Carlo)和时序差分(Temporal-Difference)
标签:根据 获得 math bubuko 随机选择 rsa算法 方法 直接 limit
原文地址:https://www.cnblogs.com/yijuncheng/p/10138542.html