LC 272. Closest Binary Search Tree Value II

标签：lower   poc   chm   暴力   思路   中序   位置   ota   基本   

Given a non-empty binary search tree and a target value, find k values in the BST that are closest to the target.

Note:

• Given target value is a floating point.
• You may assume k is always valid, that is: k ≤ total nodes.
• You are guaranteed to have only one unique set of k values in the BST that are closest to the target.

Example:

Input: root = [4,2,5,1,3], target = 3.714286, and k = 2

    4
   /   2   5
 / 1   3

Output: [4,3]

Follow up:
Assume that the BST is balanced, could you solve it in less than O(n) runtime (where n = total nodes)?

又是只会暴力求解的我T T。

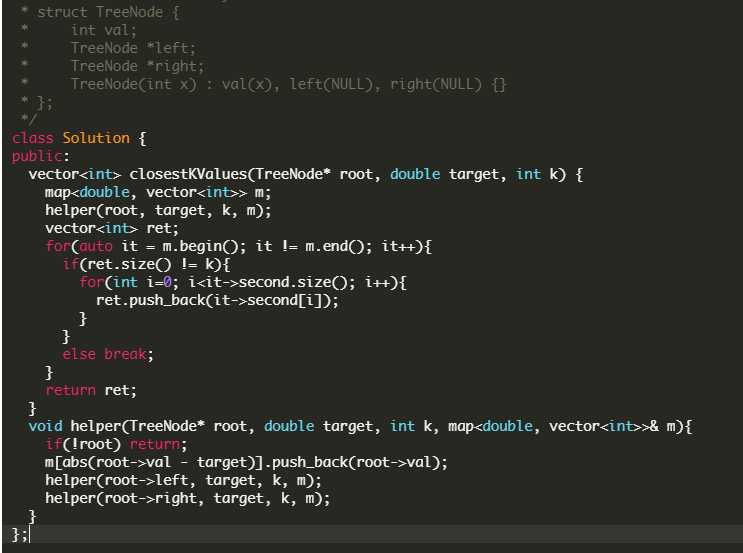
最简单的一个思路就是递归带一个order map，key是差值，value是一个vector，把所有差值存起来。最后遍历一边，因为一定是只有K个解，所以只要遍历到结果数组中元素是K个就停。

递归的时间是O(n)，遍历的时间也是O(n)

Runtime 20ms  Beats: 5.34%

当然存在更好的解法啦。

题目说小于o(n)，那一定有o(logn)的解法，想想也是，如果这不是一颗树，是一个数组应该怎么找呢，首先用lowerbound找到这个值，然后向两边扩散依此加入K个。

那如果是一颗树，应该也是可以这么做的，过程稍微复杂一点，参考了StefanPochmann大神的帖子。Stefan大神每一个帖子都能让我有重生的感觉（这代码是人写出来的？？），真的很佩服他。

在此先截一张图，看一看大家对Stefan的敬仰

哈哈哈哈

好了言归正传，先把代码放上来

基本思路就是，首先我们找到一条通往与target最近的一个path，记录下所有节点，然后向两边延申。

难点在于，树怎么延伸？其实问题转化为，在一个二叉搜索树中给定一个节点，怎么求比他大的第一个节点和比他小的第一个节点。

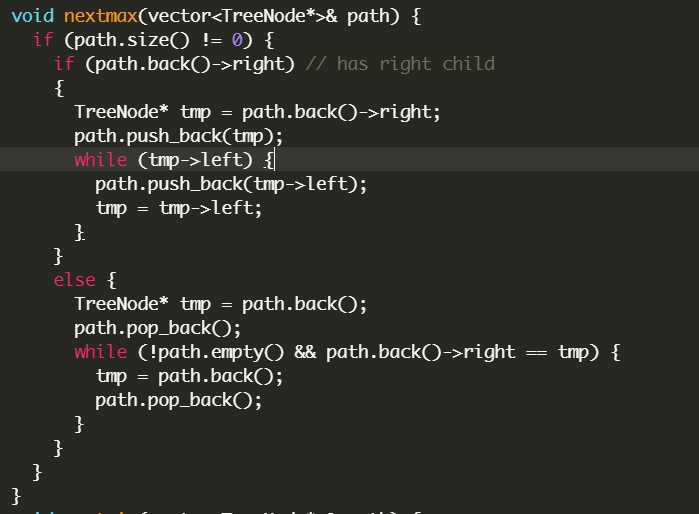
求比他大的第一个节点

分类讨论，如果这个节点存在右子节点，那么比他大的第一个节点就是右子节点的最左节点，否则，不断的回溯之前的路径，直到前一个节点

不是当前节点的右子节点（而是他的左子节点），因为当当前节点和路径的前一个节点是父节点和左子节点的关系时才会存在父节点大于原来路径中的节点的情况。

求比他小的就呼之欲出了

stefan没有重新写一遍，而是用了两个lambda函数，交换了一下位置，就把意思反过来了。

之后就是不断的更新即可。

整个过程，寻找path o(log(n))，向两边沿申最坏情况也是O（log(n)）因为题目已经说了是平衡二叉树。

下面给出我的实现。

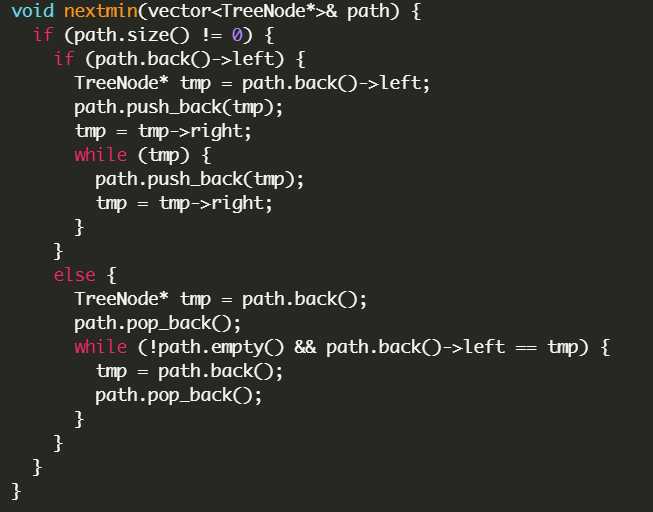
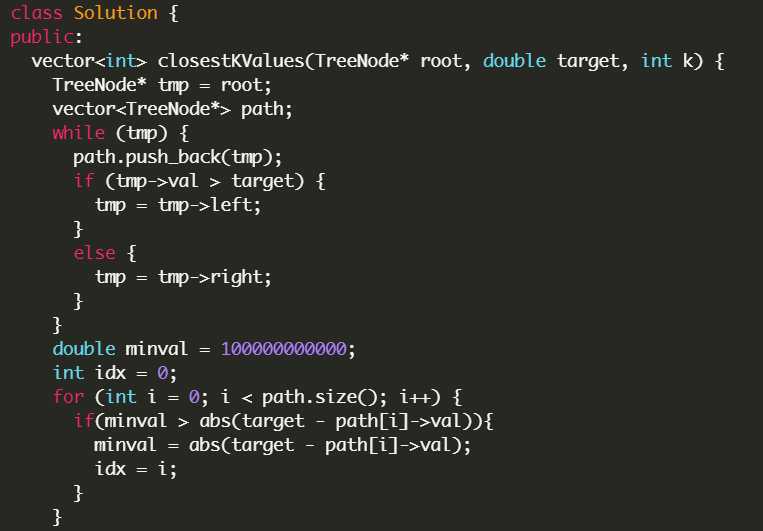
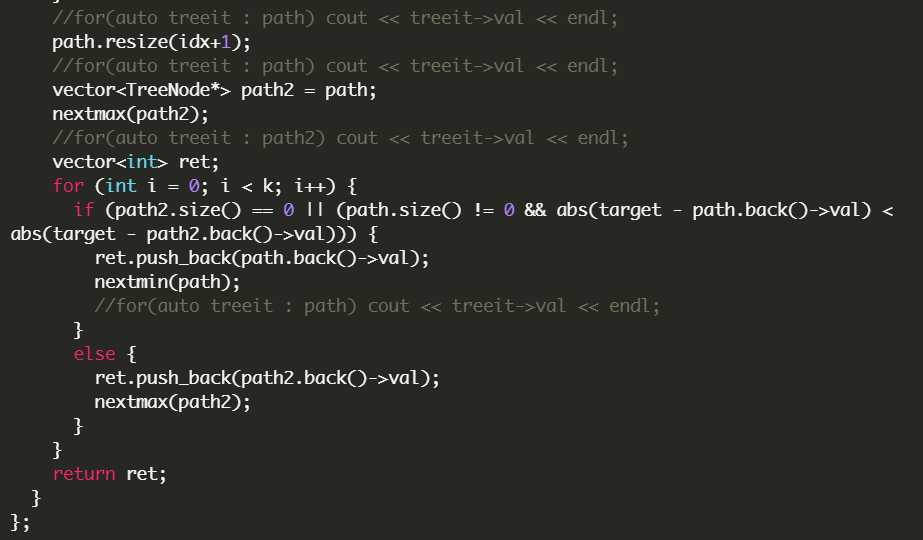
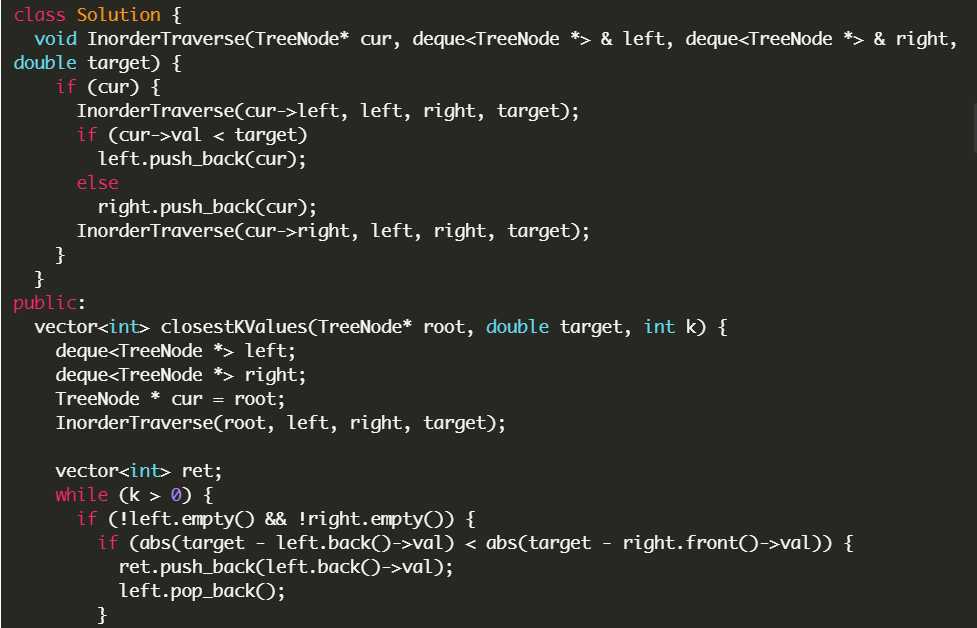
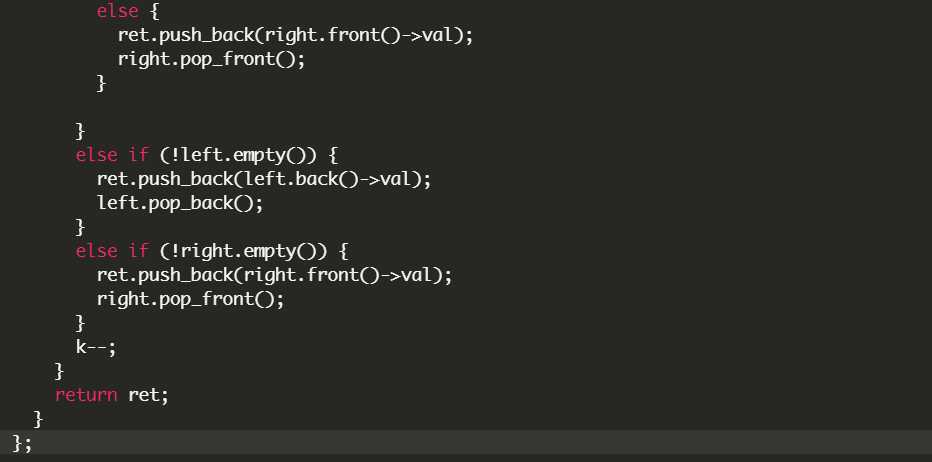
另一种解法是中序遍历，然后利用两个双端队列，小于k的存一个，大于k的存另一个，然后从两边展开，这个思路好像更容易一点，而且竟然时间更快，

理论上因为有中序遍历，这个时间复杂度是O(n)的。

LC 272. Closest Binary Search Tree Value II

标签：lower   poc   chm   暴力   思路   中序   位置   ota   基本   

原文地址：https://www.cnblogs.com/ethanhong/p/10153576.html