快速傅里叶变换

标签：次方   load   平面   9.png   计算   int   重点   代码   img   

关于复数

2次方程的求根公式

$$ax^2+bx+c=0(a\neq0)$$
$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$

3次方程（无2次项）的求根公式

$$x^3=mx+n$$
$$x=\sqrt[3]{\frac{n}{2}+\sqrt{({\frac{n}{2}})^2-({\frac{m}{3}})^3}}+\sqrt[3]{\frac{n}{2}-\sqrt{({\frac{n}{2}})^2-({\frac{m}{3}})^3}}$$

复数定义

形如$z=a+bi$的数就是复数
记作：$a=Re(z),b=Im(z)$

复数的计算

复数的几何形式

复平面，x轴为实轴，y轴为虚轴。
虚数的模，$|z|=\sqrt{a^2+b^2}$
极坐标，$z(r,\theta)$
极坐标的复数相乘，$(r1,\theta1)(r2,\theta2)=(r1r2,\theta1+\theta2)$

关于DFT

点值表示法

把这个多项式理解成一个函数，用这个函数上的若干个点的坐标来描述这个多项式。
f(x)={(x0,f(x0)),(x1,f(x1)),(x2,f(x2)),...,(xn?1,f(xn?1))}
你会得到n+1个方程，其中x[0~n]和y[0~n]是已知的， a[0~n]是未知的。
n+1的未知数， n+1个方程所组成的方程组为“n+1元一次方程”，因为它是“一次方程”，所以（一般情况下，不考虑无解和无数解）可以通过“高斯消元”解得所有未知数唯一确定的值。
也就是说，用点值表示法可以确定出唯一确定的系数表示法中的每一位的系数。

傅里叶变换

这种把一个多项式转化成“离散的点”表示的方法就叫做“DFT”（离散傅里叶变换）。
把“离散的点”还原回多项式的方法就叫做“IDFT” （离散傅里叶反变换）。

多项式乘法

单位根

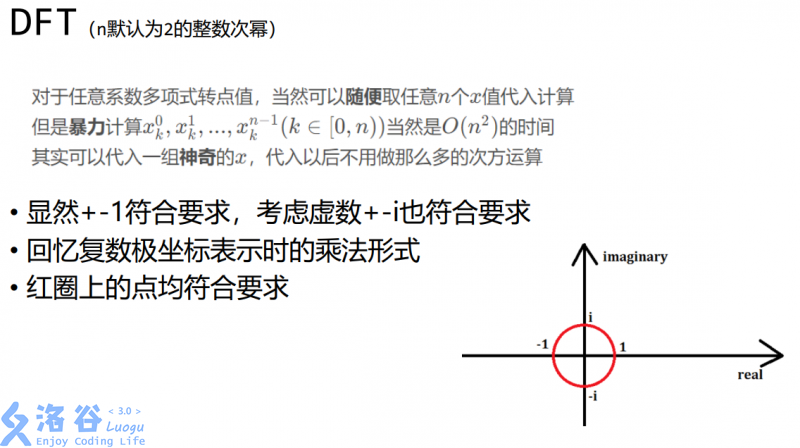
这里选择单位根（模为1的点的集合）上的点是因为$x^2=1$

关于FFT

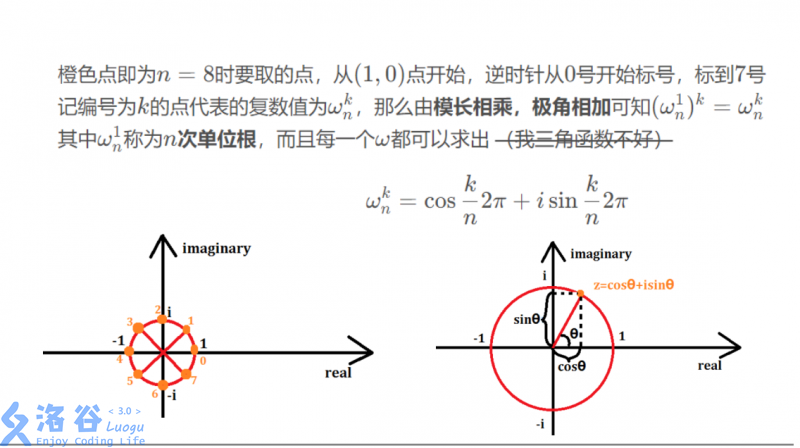
这里便是利用奇偶性进行分治，通过下面的公式推导使运算加快。



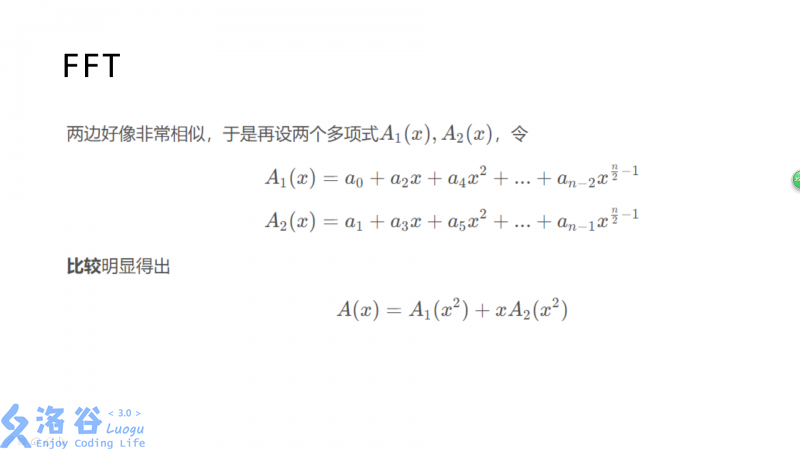
这是FFT分治的重点，他利用前面提到的单位根的性质，将每次计算的时间变成了一半，这边是FFT分治的关键。
伪代码：

FFT(a)
{
    n=a.length;
    if(n==1)
    {
        return a;
    }
    e=(a[0],a[2],...,a[n-2]);
    o=(a[1],a[3],...,a[n-1]);
    y_e=FFT(e);
    y_o=FFT(o);
    for(int k=0;k<=n/2-1;++k)
    {
        w=e^(2*π*i*k/n);
        y[k]=y_e[k]+w*y_o[k];
        y[k+n/2]=y_e[k]-w*y_o[k];
    }
}

关于IDFT

……（未完待续）

快速傅里叶变换

标签：次方   load   平面   9.png   计算   int   重点   代码   img   

原文地址：https://www.cnblogs.com/Point-King/p/10159024.html