第五章实践报告

标签：std   算法   name   alt   回溯   空间   组成   元素   接下来   

1、实践题目：工作分配问题

2、问题描述：

设集合S={x1,x2,…,xn}是一个正整数集合，c是一个正整数，子集和问题判定是否存在S的一个子集S1，使S1中的元素之和为c。试设计一个解子集和问题的回溯法。

输入格式:

输入数据第1行有2个正整数n和c，n表示S的大小，c是子集和的目标值。接下来的1行中，有n个正整数，表示集合S中的元素。 是子集和的目标值。接下来的1 行中，有n个正整数，表示集合S中的元素。

输出格式:

输出子集和问题的解，以空格分隔，最后一个输出的后面有空格。当问题无解时，输出“No Solution!”。

在这里给出一组输入。例如：

3
10 2 3
2 3 4
3 4 5

输出样例:

在这里给出相应的输出。例如：

9

3、算法描述：

本道题的解空间由长度为 n 的向量组成，第 i 个向量的取值为 j 个工人完成第 i 个任务所需的费用。以样例作解释，画出其解空间树为：

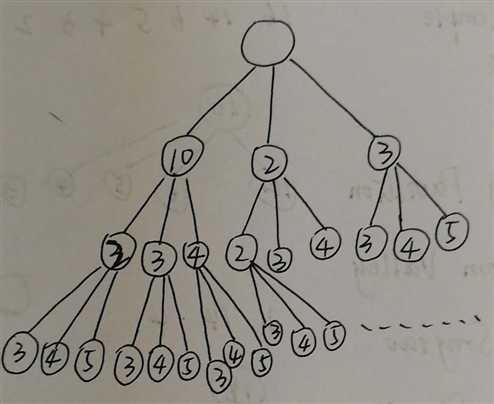
用数组 vis[n] 来判断是否第 j 个工人已经被分配了工作，初始化数组为0，如果已经被分配了工作则置为1。利用该数组进行约束剪枝。

限界函数利用两个int类型的变量 cnt 和 ans，cnt 表示当前的花费，初始化为0，ans 作为最终答案，初始化为 for（int i = 1; i <= n; i++） ans += a[i][i]。如果cnt 小于ans，那么就更新ans。

附上代码：

#include<bits/stdc++.h>
using namespace std;
int n,ans;
int a[25][25];
int vis[25];
void backtrack(int t,int cnt)
{
	if(now>n&&cnt<ans)
	{
		ans=cnt;
		return ;
	}
	if(cnt<ans)
	for(int j=1;j<=n;j++)
		if(vis[j]==0)
		{
			vis[j]=1;
			backtrack(t+1,cnt+a[t][j]);
			vis[j]=0;
		}
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			cin>>a[i][j];
			vis[j]=0;
		}
		ans+=a[i][i];
	}
	backtrack(1,0);
	cout<<ans<<endl;
}

4、心得体会：

总的来说，这次实践让自己明白了自己在回溯法的学习上还是不够的，需要更深一步的理解才行。因为在编程的时候发现自己花费的时间还是比较长的。

第五章实践报告

标签：std   算法   name   alt   回溯   空间   组成   元素   接下来   

原文地址：https://www.cnblogs.com/xwl2333/p/10160891.html