标签:个人 pre png math 代码 一个栈 queue 窗口 下标
建议不了解STL的读者先了解几个基本的队列的STL.这也是单调队列和单调栈一般都会用到的.
单调队列:建立一个队列,使队列一直具有单调性(满足单调递增或者单调递减),时间复杂度O(N).
那么我们应该如何做到"使队列一直具有单调性"呢?
以单调递增为例,我们O(N)扫描整个序列,每扫描到一个元素:
1 如果该元素大于等于队列末尾元素,则直接入队;
2 而如果该元素小于已有队列的末尾元素,即不满足单调递增,则使队列中的末尾元素出队,直到该元素符合入队条件,然后入队.
如果只到这里,那么我们仅仅做到的是最后得到了一个单调队列,是求不出题目所要求的答案的,所以我们需要在第2种情况时,在每次出队前或者出队时,维护一些我们需要的信息(如队列的长度,队列的最值等).
单调栈其实就是队列变成栈,没有太大差别.
先来看两道一模一样的例题.
输入一个长度为\(n\)的整数序列,从中找出一段不超过\(m\)的连续子序列,使得整个序列的和最大.
分析:
计算"区间和"问题,很容易想到转化为两个前缀和相减的形式.
设\(sum[i]\)表示序列前i项的和,则区间\([l,r]\)的和即为\(sum[r]-sum[l-1]\).所以我们现在就是要求出l,r,使得\(sum[r]-sum[l]\)最大,并且\(r-l<=m\).(你也可以理解为找到一组l,r,使得\(sum[r]-sum[l-1]\)最大,并且\(r-l+1<=m\))
我们枚举右端点\(i\),当i固定时,问题进一步转变为找到一个左端点\(j\),使得\(sum[j]\)最小(这样才能保证\(sum[i]-sum[j]\)最大),同时注意\(j\)的位置是在\([i-m,i-1]\)上.
此时单调队列的核心来了:
假设有一个位置\(k\)和\(j\),如果\(k<j<i\)并且\(sum[k]>=sum[j]\),那么对于所有大于等于\(i\)的右端点,\(j\)一定是比\(k\)更好的一个左端点.因为\(j\)比\(k\)在位置上更靠近\(i\),更不容易超过序列长度\(m\)的限制,而且\(sum[j]\)比\(sum[k]\)还小,更符合序列和最大的性质.
我们可以戏称为"一个人比你小还比你强,你就废了".
其实这就是单调队列的思想:及时排除一定不是最优解的解.
int l=1,r=1;
//队列左右端点初始化
q[1]=0;
//队列第1号元素赋值为零,防止下标越界
for(int i=1;i<=n;i++){
while(l<=r&&q[l]<i-m)l++;
//如果队头位置与当前右端点i的距离超过m,出队
ans=max(ans,sum[i]-sum[q[l]]);
//此时队头就是右端点为i时,左端点j的最优选择
//这里我想详细讲一下为什么看似只满足序列长度
//不超过m的队头一定是最优解
//根据上面核心算法可知,这个队头被保留了下来
//一定是因为它的sum比它后面的sum小
//否则它就是那个又老又弱的元素,早就被淘汰了
//它既然留了下来,说明它虽然老,但是老当益壮
while(l<=r&&sum[q[r]]>=sum[i])r--;
q[++r]=i;
//i作为右端点的情况讨论完了
//此时它需要被作为将来的左端点而入队
//而在它入队前我们需要淘汰掉那些
//比它老还比它弱的东西
}滑动窗口:
现在有一堆数字共\(N\)个数字(\(N<=10^6\)),以及一个大小为\(k\)的窗口。现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。
分析:上题是求区间和最大值,本题是求区间最值,应该也算是很经典的模板题了吧,为了推广一下STL,我用了STL的队列,当然也可以像上题那样数组模拟队列.
以求区间最大值为例:
deque<int> q;
//建立一个双端队列
for(int i=1;i<=n;i++){
while(!q.empty()&&a[i]<a[q.back()])
q.pop_back();
q.push_back(i);
//在把当前元素i入队前我们需要淘汰掉那些
//比它老还比它弱的东西
while(q.front()<=i-k)
q.pop_front();
//如果队头位置与当前右端点i的距离超过k,出队
ans1[i]=a[q.front()];
//记录下当前窗口下的最大值
for(int i=k;i<=n;i++)
printf("%d ",ans1[i]);
//注意一下输出范围
}工作调度:
在任一时刻可以选择\(n\)项工作中的任意一个工作来做,每项工作花一个单位时间,对于第\(i\)个工作,截止时间\(d[i]\),获利\(p[i]\).
分析:把n个工作按照截止时间从小到大排序,根据单调队列的思想,建立一个小根堆
priority_queue<int,vector<int>,greater<int> >q;对于第i项工作,如果队列(小跟堆)中的元素个数小于它的截止时间\(a[i].x\),直接入队(小跟堆),同时最大获利ans累加\(a[i].y\).
如果队列(小跟堆)中的元素个数大于等于它的截止时间\(a[i].x\),与队首(堆顶)元素比较获利值,谁大谁留下.
同时记得更新ans值和队列(小跟堆)
for(int i=1;i<=n;i++){
if(a[i].x<=q.size()){
if(a[i].y>q.top()){
ans=ans+a[i].y-q.top();
q.pop();
q.push(a[i].y);
}
}
else{
q.push(a[i].y);
ans+=a[i].y;
}
}一道很容易的省选题:小组队列
有\(m\)个小组,\(n\)个元素,每个元素属于且仅属于一个小组。
支持以下操作:
push x:使元素x进队,如果前边有x所属小组的元素,x 会排到自己小组最后一个元素的下一个位置,否则x排到整个队列最后的位置。
pop:出队,弹出队头并输出出队元素,出队的方式和普通队列相同,即排在前边的元素先出队。
分析:建立两个队列queue,一个维护整个大队列(即只有小组组号的队列),另一个维护对于大队列中的每个元素(即每个小组)内部的元素.
如图所示,在一条水平线上有n个宽为1的矩形,求包含于这些矩形的最大子矩形面积(图中的阴影部分的面积即所求答案)。
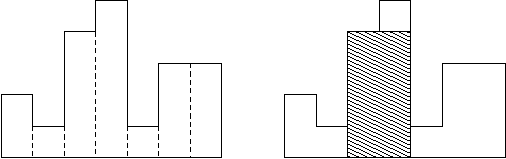
根据单调队列的思想,建立一个栈,用来保存若干个矩形,这些矩形的高度是单调递增的.从左到右依次扫描每个矩形:
1 如果当前矩形比栈顶矩形高,直接进栈
2 否则,不断把栈内比当前矩形高的的矩形出栈,直到栈为空或者栈顶矩形的高度比当前矩形小.在出栈过程中,累计被弹出的矩形的宽度之和,并且每弹出一个矩形,就用该矩形的高度乘上以经累计的宽度去更新答案max.整个出栈过程结束后,把高度为当前扫描到的矩形高度,宽度为累计宽度的新矩形入栈.
3 整个扫描结束后,还要计算栈内剩余矩形能够构成的最大矩形面积,方法跟步骤2类似.
第2步看文字不理解的话,建议手画几个高矮不齐的矩形根据代码模拟一下,一定要弄懂,这是单调栈的核心思想.
while(~scanf("%d",&n)){
if(!n)break;
int top=0;
//模拟栈顶指针
long long ans=0;
//记录最大面积ans
for(int i=1;i<=n;i++)h[i]=read();
//读入每个矩形的高度
h[n+1]=0;
//这是一个为了实现第3步的小技巧
for(int i=1;i<=n+1;i++){
if(h[i]>=st[top]){
top++;
st[top]=h[i];
wid[top]=1;
}
//如果当前扫描到的矩形的高度比栈顶矩形高度大
//直接把当前矩形入栈,同时该矩形宽度设为1
else{
int width=0;
while(st[top]>h[i]){
width+=wid[top];
//累计出栈矩形高度
ans=max(ans,(long long)width*st[top]);
//同时把该出栈矩形的高度乘累计宽度以更新最大值
top--;
}
st[++top]=h[i];
wid[top]=width+1;
//把高度为当前扫描到的矩形的高度
//宽度为累计宽度的新矩形入栈
}
}
printf("%lld\n",ans);
}标签:个人 pre png math 代码 一个栈 queue 窗口 下标
原文地址:https://www.cnblogs.com/PPXppx/p/10161699.html