第五章上机实验报告

标签：题目   练习   剪枝   问题   span   存在   通过   strong   distrib   

1.     实践题目及问题描述

工作分配问题；n件工作分配给n个人，为每一个人都分配1 件不同的工作，工作i分配给第j个人所需的费用为cij，设计一个算法，使总费用最小。

2.     算法描述

（1）     解空间

{<x11,x12…x1n>,<x21,x22…x2n>……<xn1,xn2…xnn>}

其中 <x11,x12…x1n>!=<x21,x22…x2n>!=…!= <xn1,xn2…xnn>

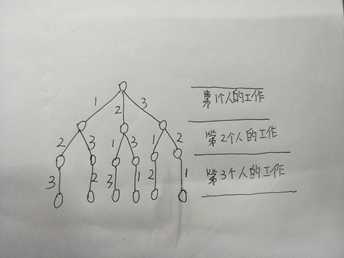
（2）     解空间树（n=3为例）

（3）     剪枝方法描述

限界函数：当给所有人分配完工作后就返回

if(t == n+1){

          if(cost < best){

                 best = cost;

                 return;

          }

      }

约束函数：当前总费用大于记录的最少费用时回溯，不再往下遍历

if(cost < best){

                 distribution(t+1);

          }

swap(x[t],x[i]);

cost -=c[t][x[i]];

3.     心得体会

觉得这章的回溯法代码比较难理解，不怎么会打，但通过上机课多打对回溯法有了进一步的了解。然而还是存在疑惑，有些代码不知道是怎么回溯的，可能是之前学的调用方法还没学透。有待多练习。

第五章上机实验报告

标签：题目   练习   剪枝   问题   span   存在   通过   strong   distrib   

原文地址：https://www.cnblogs.com/lyt823/p/10162293.html