标签：变量   pre   des   价格   img   white   技术分享   输入   bubuko   

引例：以房价和房屋面积作为训练集，学习如何预测房价

• m 代表训练集的数量
• x 代表输入变量(特征)，这里代表房屋面积
• y 代表输出变量(标签)，这里代表房价
• (x, y)表示一个训练样本
• (x^(i), y^(i))表示第i个训练样本

单变量线性回归算法的实现过程

• 训练集(房屋面积x, 房价y)— —>学习算法— —>h(x)假设函数
• 房屋面积(x)— —>h(x)假设函数— —> 预测房价(y)
• 假设函数：h(x) = w1x + b

单变量线性回归最常用的损失函数：均方误差MSE

假设函数和房屋价格的实际价格的差值，差值越小损失越小

均方误差(MSE) = ∑(h(x)-y)^2/m

　　　　　= ∑(w1x + b -y)^2/m

                  =J(w1, b), 其中 x∈(1, m) 

即求一组w1,b使J(w1, b)(MSE)最小

• (x, y)代表样本
• x 代表输入变量(特征)，这里代表房屋面积
• y 代表输出变量(标签)，这里代表房价
• m 代表训练集(样本)的数量
• w1代表权重，b代表偏差(y轴截距)

假设函数和损失函数

• h(x) = w1x + b, x是变量
• J(w1, b) = ∑(w1x+b-y)^2/m，w1, b是变量

梯度下降Gradient descent

对于J(w1, b)初始化选择任意w1,b，慢慢改变w1,b的值使得J(w1, b)取得最小值或者局部最小值

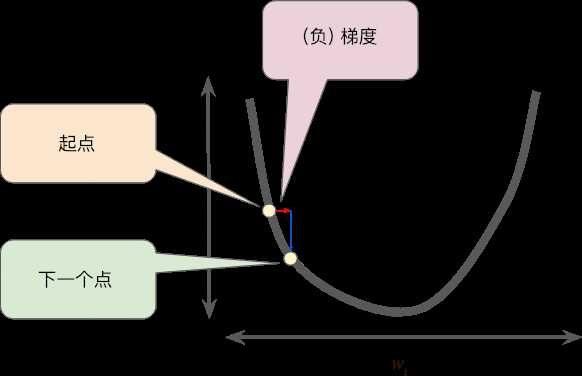
梯度下降w1的值变化：  w1 := w1 - aJ(w1,b)’， 对于此方程当J(w1,b)’ 为0时w1不变，即找到最小值或者局部最小值

• 其中 := 赋值
• a 学习速率(learning rate)
• J(w1,b)’ :函数在w1, b点的导数

学习速率learning rate

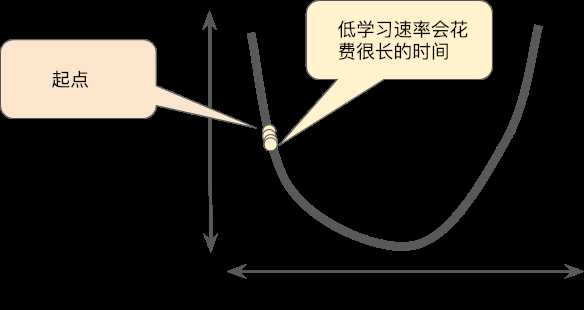
学习速率过小

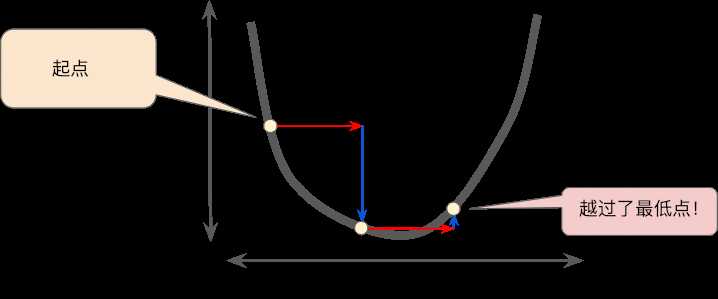
学习速率过大

线性回归算法实现

结合假设函数、损失函数、梯度下降函数

• h(x) = w1x + b
• J(w1, b)=∑(w1x + b -y)^2/m
• w1 := w1 - aJ(w1,b)’

得出线性回归算法：

• w1 := w1 - 2ax∑(w1x + b -y)^/m
• b:=b- 2a∑(w1x + b -y)^/m

W1和b同时更新

2、单变量线性回归

标签：变量   pre   des   价格   img   white   技术分享   输入   bubuko   

原文地址：https://www.cnblogs.com/jp-mao/p/10163141.html