标签:分享图片 col names 开始 bsp ons code pac 根据

答案参考来自 http://www.cnblogs.com/sugewud/p/9822933.html
思路:思维题OR规律题?个人没写出来,脑子里只有深度DFS暴力,看完了一个大佬的题解,学到了思路ANDpow()函数的另一种写法,妙不可言!
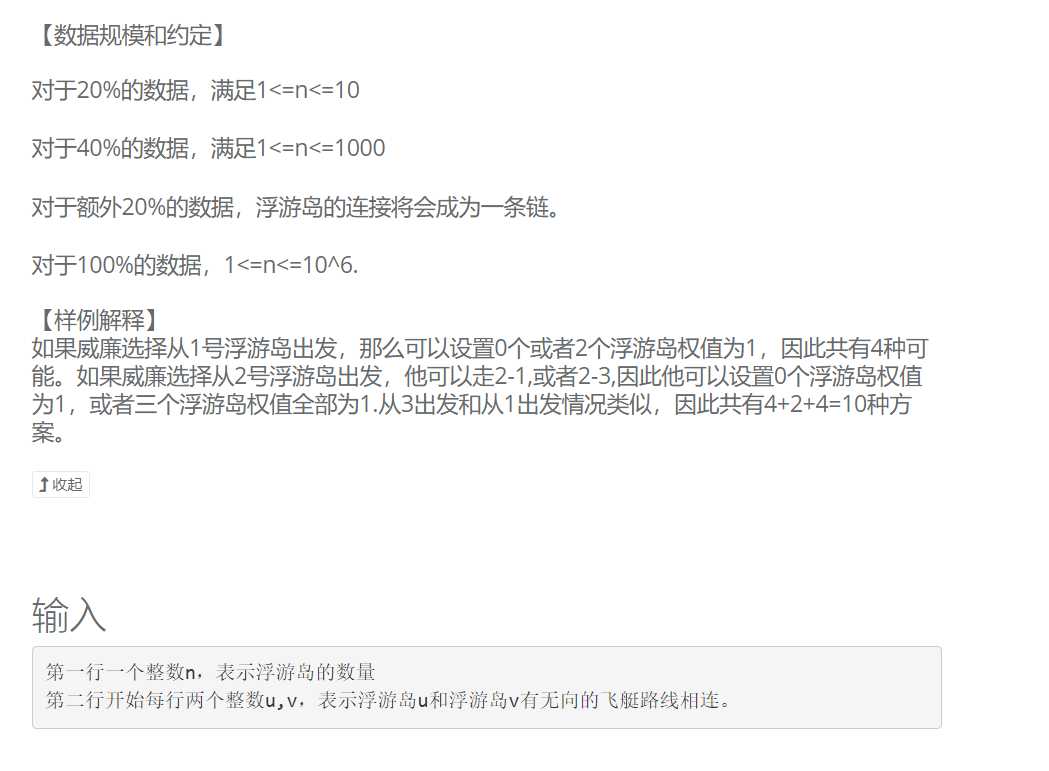
先说思路:从一条链的时候开始推导,假如这条链长度为n,这条链上面的点分为两种—端点和非端点;
先看非端点的情况 0-0-0-0-0-0-0-0-0-0-0
其中的某一个非端点,到达两个端点的情况是2^(n-2),也就是说这个非端点到达一个端点的时,除去这个端点的的路上非端点的值01都行,最后到达端点时根据01的情况来确定端点值,所以端点值是确定的,那么到达两个端点的情况加起来就是2^(n-2)。
再来看端点的情况,0-0-0-0-0-0-0-0-0-0-0-0
只需考虑一个端点到达另一个端点,在该端点到达另外一个端点的路上,也就是说包含了一个端点和所有的非端点,这些端点值都是可以任意取值的,最后到达另一个端点时根据当前01的情况来考虑另一个端点的值,也就是说另一个端点的值其实是已经确定了的,这样的话情况就是2*2^(n-1)。
上面是两个端点的情况,以此类推到k个端点的情况,可以得到最后的答案是(n+k)*2^(n-k);
再来说一下pow()函数,直接上代码,我觉得很好需要保存一下
ll pow(ll a, int b) { ll res = 1 % mod; a %= mod; for(; b; b >>= 1) { if(b & 1) res = res * a % mod; a = a * a % mod; } return res; }
以下是我写的题解(算不算我写的呢??),提交的时候发现会卡cin输入
#include<cstring> #include<iostream> #define _ 0 #define ll long long using namespace std; const int maxn = 1e6 + 10; const int mod = 1e9 + 7; int d[maxn]; inline ll poow(int x, int nn){ ll sum = 1; for (int i = 0; i < nn; i++){ sum = (sum*x) % mod; } return sum; } int main(){ ios::sync_with_stdio(false); int n; while (cin >> n){ if (n == 1)return puts("1"), 0; memset(d, 0, sizeof d); for (int i = 0; i < n - 1; i++){ int u, v; cin >> u >> v; d[u] += 1; d[v] += 1; } int k = 0; for (int i = 1; i <= n; i++) if (d[i] == 1)k += 1; cout << 1LL * (n + k)*poow(2, n - k) % mod << endl; } return ~~(0 ^ _ ^ 0); }
标签:分享图片 col names 开始 bsp ons code pac 根据
原文地址:https://www.cnblogs.com/zengguoqiang/p/10164168.html