标签:奇异值分解 课程 unit 网络 expec exp arc 均值 衡量
Lecture 7 神经网络二
课程内容记录:https://zhuanlan.zhihu.com/p/21560667?refer=intelligentunit
1.协方差矩阵:
协方差(Covariance)在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。
协方差表示的是两个变量的总体的误差,这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
期望值分别为E[X]与E[Y]的两个实随机变量X与Y之间的协方差Cov(X,Y)定义为:
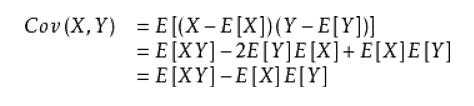
如果X与Y是统计独立的,那么二者之间的协方差就是0,因为两个独立的随机变量满足E[XY]=E[X]E[Y]。
但是,反过来并不成立。即如果X与Y的协方差为0,二者并不一定是统计独立的。
方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。在许多实际问题中,研究方差即偏离程度有着重要意义。
在概率分布中,设X是一个离散型随机变量,若E{[X-E(X)]^2}存在,则称E{[X-E(X)]^2}为X的方差,记为D(X),其中E(X)是X的期望值,X是变量值,公式中的E是期望值expected value的缩写,意为“变量值与其期望值之差的平方和”的期望值。离散型随机变量方差计算公式:
D(X)=E{[X-E(X)]^2}=E(X^2) - [E(X)]^2
当D(X)=E{[X-E(X)]^2}称为变量X的方差,而σ=(D(X))^0.5 称为标准差(或均方差)。它与X有相同的量纲。标准差是用来衡量一组数据的离散程度的统计量。
参见:https://www.cnblogs.com/terencezhou/p/6235974.html
参见:https://blog.csdn.net/mr_hhh/article/details/78490576
2.半正定矩阵:
半正定矩阵是正定矩阵的推广。实对称矩阵A称为半正定的,如果二次型X‘AX半正定,即对于任意不为0的实列向量X,都有X‘AX≥0。
3.主成分分析:(PCA)
参见:https://www.cnblogs.com/pinard/p/6239403.html
4.奇异值分解:
奇异值分解(Singular Value Decomposition)是线性代数中一种重要的矩阵分解,奇异值分解则是特征分解在任意矩阵上的推广。
参见:https://www.cnblogs.com/pinard/p/6251584.html
参见:http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html
5.反向随机失活:
参见:https://blog.csdn.net/sinat_29957455/article/details/81023154
标签:奇异值分解 课程 unit 网络 expec exp arc 均值 衡量
原文地址:https://www.cnblogs.com/yun-an/p/10164728.html