[USACO18DEC]Balance Beam

标签：org   分享   alt   jpg   algo   php   平衡   show   www.   

题目链接：这里

或者这里

答案是很显然的，记\(g(i)\)为在\(i\)下平衡木时的期望收益

那么\(g(i)=max(f(i),\frac{g(i-1)+g(i+1)}{2})\)

好了做完了

TMD这个式子有和没有有什么区别啊（还是有区别的）

我们考察那些\(g(i)=f(i)\)的点

更特殊的，我们考虑点\((i,f(i))\)在二维坐标上的分布，同时由\(f(0)=f(n+1)=0\)我们再加入两个新点\((0,0)\)和\((n+1,0)\)

那么样例的图就是这样子的

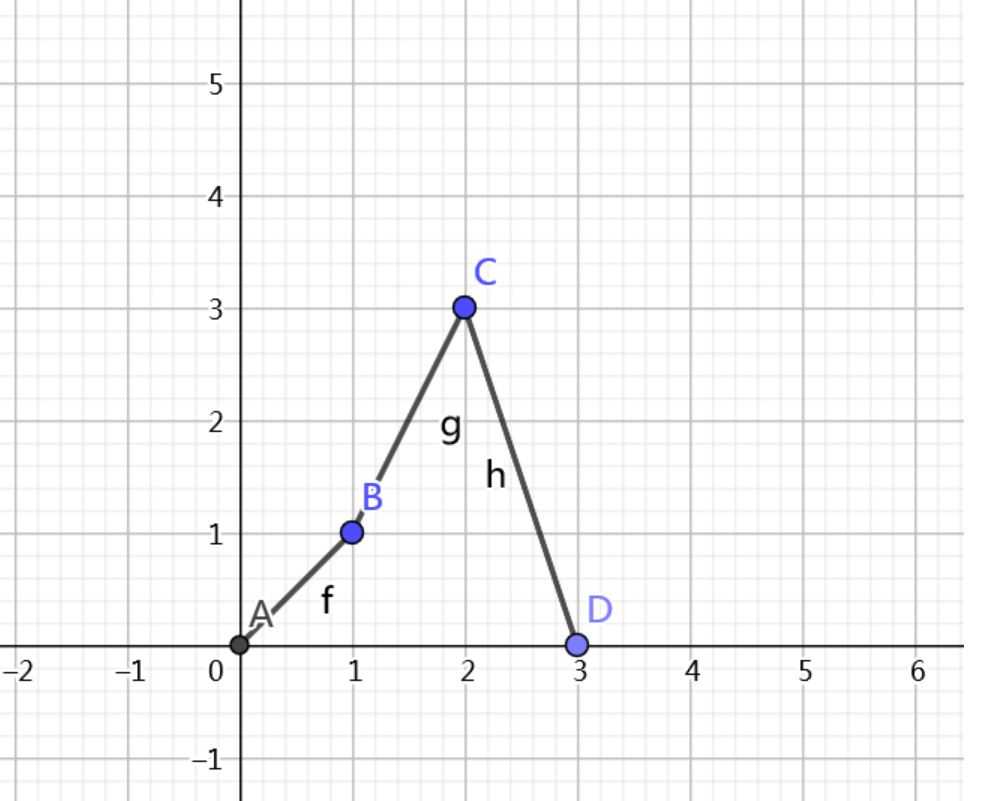
我们再来看一下期望在这个平面上的分布（图中的红线）

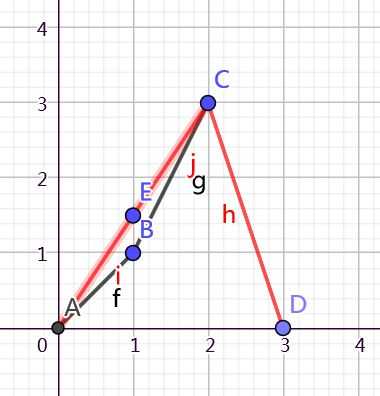
我们会发现，在1处的期望是AC两点的连线在\(x=1\)处的取值

这是不是偶然？

我们重新回到一开始的式子\(g(i)=max(f(i),\frac{g(i-1)+g(i+1)}{2})\)

\(g(i)\)就是一开始出现在图一中的点，而\(\frac{g(i-1)+g(i+1)}{2}\)则是这个点两端的点的连线在\(i\)上的取值

而我们的\(g(i)\)是在这两者之间取一个max

也就是说所有的\(g(i)\)应该在所有的\(f(i)\)的点所构成的一个上凸包上

这样我们就可以先把凸包跑出来，再记录下这个点两端的凸包的点，在凸包上的点\(f(i)\)就是其期望

其它点运用一次函数的相关知识解出期望即可

#include<iostream>
#include<string>
#include<string.h>
#include<stdio.h>
#include<algorithm>
#include<math.h>
#include<vector>
#include<queue>
#include<map>
using namespace std;
#define rep(i,a,b) for (i=a;i<=b;i++)
typedef long long ll;
#define maxd 1e5
ll f[100100],l[100100],r[100100],hull[100100];
int n,top=0;

int read()
{
    int x=0,f=1;char ch=getchar();
    while ((ch<‘0‘) || (ch>‘9‘)) {if (ch==‘-‘) f=-1;ch=getchar();}
    while ((ch>=‘0‘) && (ch<=‘9‘)) {x=x*10+(ch-‘0‘);ch=getchar();}
    return x*f;
}

int main()
{
    n=read();int i,j;
    for (i=1;i<=n;i++) f[i]=read();
    hull[++top]=0;
    for (i=1;i<=n+1;i++)
    {
        while (top>=2)
        {
            int a=hull[top],b=hull[top-1];
            //cout << top << endl;
            if ((f[a]-f[b])*(i-a)<(f[i]-f[a])*(a-b)) top--;
            else break;
        }
        hull[++top]=i;
    }
    //for (i=1;i<=top;i++) cout << hull[i] << " ";cout << endl;

    for (i=1;i<top;i++)
    {
        for (j=hull[i]+1;j<hull[i+1];j++)
        {
            l[j]=hull[i];r[j]=hull[i+1];
        }
        l[hull[i]]=hull[i];r[hull[i]]=hull[i];
    }
    l[n+1]=n+1;r[n+1]=n+1;
    //for (i=0;i<=n+1;i++) cout << l[i] << " ";cout << endl;
    //for (i=0;i<=n+1;i++) cout << r[i] << " ";cout << endl;
    for (i=1;i<=n;i++)
    {
        ll ans=0;
        if (l[i]==r[i]) ans=f[i]*maxd;
        else ans=(maxd*(f[l[i]]*(r[i]-i)+f[r[i]]*(i-l[i])))/(r[i]-l[i]);
        printf("%lld\n",ans);
    }
    return 0;
}

[USACO18DEC]Balance Beam

标签：org   分享   alt   jpg   algo   php   平衡   show   www.   

原文地址：https://www.cnblogs.com/zhou2003/p/10184511.html