标签:getchar void cpp code 还需要 algorithm 博弈论 mat clu

考虑对于每个子树从下往上依次考虑
对于叶子节点而言,如果可以染色,那么其\(sg\)值为\(1\),否则为\(0\)
考虑往上合并
如果选择了\(x\),那么后继状态就是其所有子树
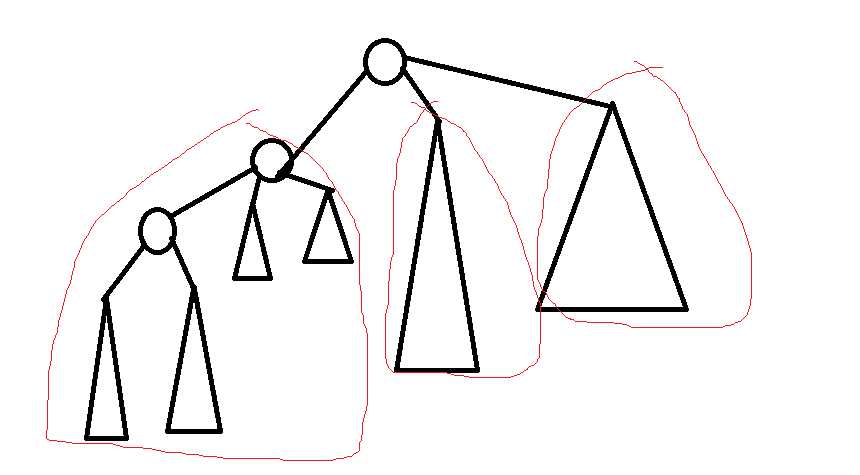
如果选了其他子树中的一点,那么后继状态的构成如图所示
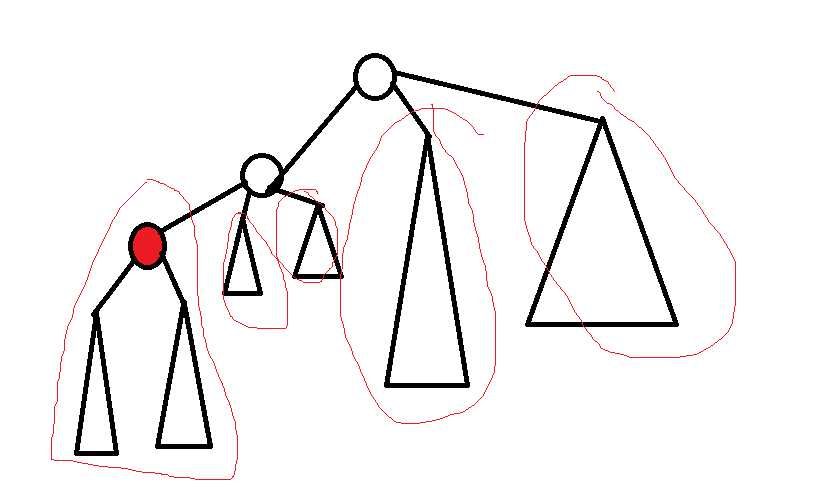
也就是,到当前根为止的所有其他子树的\(sg\)值异或上本身
那么,我们可以考虑维护一个数据结构,每次往上的时候,对于一棵子树内的点,异或上其他子树的\(sg\)值
至于查\(sg\)值,可以用一个支持查\(mex\)的东西
还需要合并
\(Trie\)树是一个不错的选择
输出答案就随意\(dfs\)一下,思路和上面的差不多
复杂度\(O(n \log n)\)
#include <map>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define ri register int
#define rep(io, st, ed) for(ri io = st; io <= ed; io ++)
#define drep(io, ed, st) for(ri io = ed; io >= st; io --)
const int sid = 2e5 + 5;
const int cid = 2e7 + 5;
#define gc getchar
inline int read() {
int p = 0, w = 1; char c = gc();
while(c > '9' || c < '0') { if(c == '-') w = -1; c = gc(); }
while(c >= '0' && c <= '9') p = p * 10 + c - '0', c = gc();
return p * w;
}
bool cov[cid];
int n, id, tot, cnp;
int q[sid], sg[sid], ls[cid], rs[cid], xr[cid];
int rt[sid], col[sid], cap[sid], nxt[sid], node[sid];
inline void addedge(int u, int v) {
nxt[++ cnp] = cap[u]; cap[u] = cnp; node[cnp] = v;
}
inline void put_xor(int &o, int val, int dep) {
if(dep <= -1) return;
if(val & (1 << dep)) swap(ls[o], rs[o]);
xr[o] ^= val;
}
inline void pushdown(int o, int dep) {
if(!xr[o] || !o) return;
put_xor(ls[o], xr[o], dep - 1);
put_xor(rs[o], xr[o], dep - 1);
xr[o] = 0;
}
inline void insert(int &o, int val, int dep) {
if(!o) o = ++ id;
if(dep == -1) { cov[o] = 1; return; }
if(val & (1 << dep)) insert(rs[o], val, dep - 1);
else insert(ls[o], val, dep - 1);
}
inline int merge(int x, int y, int dep) {
if(!x || !y) return x + y;
if(dep == -1) { cov[x] |= cov[y]; return x; }
pushdown(x, dep); pushdown(y, dep);
ls[x] = merge(ls[x], ls[y], dep - 1);
rs[x] = merge(rs[x], rs[y], dep - 1);
cov[x] = cov[ls[x]] && cov[rs[x]];
return x;
}
inline int mex(int o, int dep) {
if(!o || dep == -1) return 0;
pushdown(o, dep);
if(!cov[ls[o]]) return mex(ls[o], dep - 1);
else return (1 << dep) + mex(rs[o], dep - 1);
}
#define cur node[i]
inline void dfs(int o, int fa) {
int nsg = 0;
for(int i = cap[o]; i; i = nxt[i])
if(cur != fa) dfs(cur, o), nsg ^= sg[cur];
if(!col[o]) insert(rt[o], nsg, 17);
for(int i = cap[o]; i; i = nxt[i])
if(cur != fa) {
put_xor(rt[cur], nsg ^ sg[cur], 17);
rt[o] = merge(rt[o], rt[cur], 17);
}
sg[o] = mex(rt[o], 17);
}
inline void find(int o, int fa, int SG) {
for(int i = cap[o]; i; i = nxt[i])
if(cur != fa) SG ^= sg[cur];
if(SG == 0 && !col[o]) q[++ tot] = o;
for(int i = cap[o]; i; i = nxt[i])
if(cur != fa) find(cur, o, SG ^ sg[cur]);
}
int main() {
n = read();
rep(i, 1, n) col[i] = read();
rep(i, 2, n) {
int u = read(), v = read();
addedge(u, v); addedge(v, u);
}
dfs(1, 0);
find(1, 0, 0);
if(tot) {
sort(q + 1, q + tot + 1);
rep(i, 1, tot) printf("%d\n", q[i]);
}
else puts("-1");
return 0;
}标签:getchar void cpp code 还需要 algorithm 博弈论 mat clu
原文地址:https://www.cnblogs.com/reverymoon/p/10197772.html