标签:text nbsp open post show order 数据 计算 sub
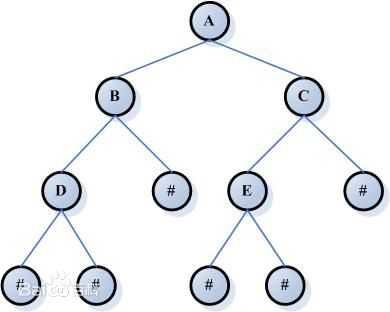
定义:在计算机科学中,二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。
二叉树的节点表示以及树的构建:
class Node: """二叉树节点类""" def __init__(self, item): self.value = item self.lchild = None self.rchild = None class Tree: """二叉树""" def __init__(self): self.root = None def add(self, item): node = Node(item) if self.root == None: self.root = node return queue = [self.root] while queue: cur_node = queue.pop(0) if cur_node.lchild is None: cur_node.lchild = node return else: queue.append(cur_node.lchild) if cur_node.rchild is None: cur_node.rchild = node return else: queue.append(cur_node.rchild)
一:层次遍历
即按照层次访问,通常用队列来做。访问根,访问子女,再访问子女的子女
二:先序遍历
我们先访问根节点,然后递归使用先序遍历去访问左子树,再递归使用先序遍历访问右子树 (根节点 左子树 右子树)
三:中序遍历
我们递归使用中序遍历去访问左子树,然后访问根节点,再递归使用中序遍历访问右子树 (左子树 根节点 右子树)
四:后序遍历
我们递归使用后序遍历去访问左子树,然后递归使用后序遍历访问右子树,再访问根节点 (左子树 右子树 根节点)
代码实现:

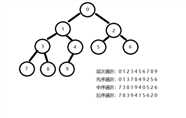
class Node: """二叉树节点类""" def __init__(self, item): self.value = item self.lchild = None self.rchild = None class Tree: """二叉树""" def __init__(self): self.root = None def add(self, item): node = Node(item) if self.root == None: self.root = node return queue = [self.root] while queue: cur_node = queue.pop(0) if cur_node.lchild is None: cur_node.lchild = node return else: queue.append(cur_node.lchild) if cur_node.rchild is None: cur_node.rchild = node return else: queue.append(cur_node.rchild) def level_travel(self): """层次遍历,广度优先 从树的根节点开始 从上到下从左到右遍历整个树的节点 """ if self.root is None: return queue = [self.root] print(self.root.value, end=‘ ‘) while queue: cur_node = queue.pop(0) if cur_node.lchild is not None: print(cur_node.lchild.value, end=‘ ‘) queue.append(cur_node.lchild) if cur_node.rchild is not None: print(cur_node.rchild.value, end=‘ ‘) queue.append(cur_node.rchild) def pre_order(self, node): """先序遍历""" if node is None: return print(node.value, end=‘ ‘) self.pre_order(node.lchild) self.pre_order(node.rchild) def inorder(self, node): """中序遍历""" if node is None: return self.inorder(node.lchild) print(node.value, end=‘ ‘) self.inorder(node.rchild) def postorder(self, node): """后序遍历""" if node is None: return self.postorder(node.lchild) self.postorder(node.rchild) print(node.value, end=‘ ‘) tree = Tree() tree.add(0) tree.add(1) tree.add(2) tree.add(3) tree.add(4) tree.add(5) tree.add(6) tree.add(7) tree.add(8) tree.add(9) tree.breadth_travel() # 0 1 2 3 4 5 6 7 8 9 print(‘‘) tree.pre_order(tree.root) # 0 1 3 7 8 4 9 2 5 6 print(‘‘) tree.inorder(tree.root) # 7 3 8 1 9 4 0 5 2 6 print(‘‘) tree.postorder(tree.root) # 7 8 3 9 4 1 5 6 2 0
图解:
标签:text nbsp open post show order 数据 计算 sub
原文地址:https://www.cnblogs.com/yeyangsen/p/10197917.html