标签：和我 alt ati 概率 技术 表示 展开 等于 年龄
一个栗子
数据：工资和房屋面积（2个特征）
目标：预测银行会贷款给我多少钱（标签）
考虑：工资和房屋面积都会影响最终银行贷款的
结果那么它们各自有多大的影响呢？（参数）
| 姓名 | 工资(元) | 房屋面积(平方米) | 可贷款金额(元) |
|---|---|---|---|
| 张三 | 6000 | 58 | 30000 |
| 李四 | 9000 | 77 | 55010 |
| 王五 | 11000 | 89 | 73542 |
| 陆永剑 | 15000 | 54 | 63201 |
通俗解释
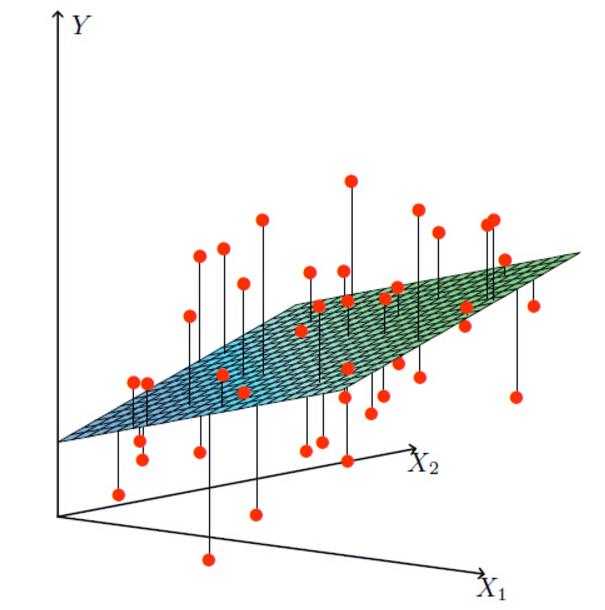
X1,X2就是我们的两个特征（年龄，房屋面积）Y是银行最终会借给我们多少钱
找到最合适的一条线（想象一个高维）来最好的拟合我们的数据点
假设 
是年龄的参数， 
是房屋面积的参数
拟合的平面：
（
是偏置项）
整合：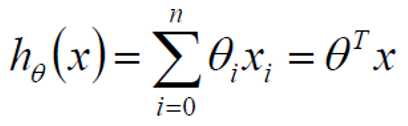
真实值和预测值之间肯定是要存在差异的（用
来表示该误差）
对于每个样本
误差 
是独立并且具有相同的分布，并且服从均值为0方差为
的高斯分布
独立：张三和李四一起来贷款，他俩没关系
同分布：他俩都来得是我们假定的这家银行
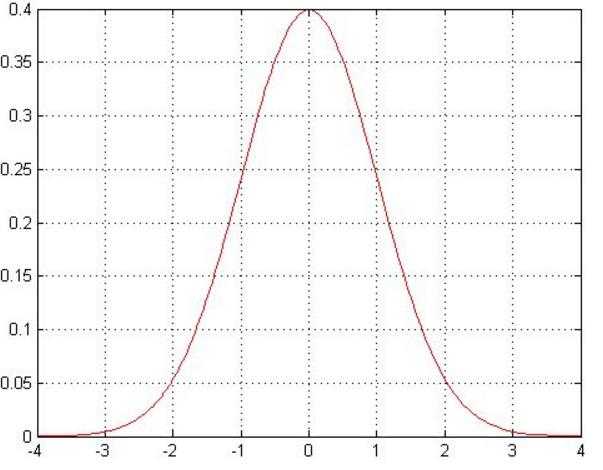
高斯分布：银行可能会多给，也可能会少给，但是绝大多数情况下
这个浮动不会太大，极小情况下浮动会比较大，符合正常情况
预测值与误差： 
由于误差服从高斯分布： 
带入：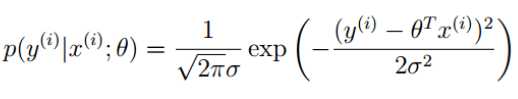
高斯分布的积分为1，所以可以把闭区间的面积看作概率，中间区域的面积最大，说明值落在中间的概率大，由图可知，有大概率的点是落在x=0附近的，高斯分布的纵坐标无实际意义，纵坐标的值与方差θ的平方有关，θ越大，表示样本的震荡幅度越大（不会密集的分布在0附近），那么图像就越矮，纵坐标越小。
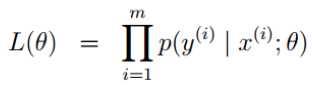
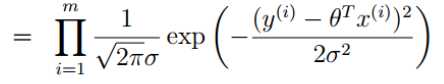
目的：计算出什么样的参数θ和我们的数据(x,y)组合之后，能满足我们的真实值
形象理解：比如说我们掷硬币，掷了十次，结果是九次正面朝上，一次反面朝上，那么认为下一次正面朝上的概率θ就是90%；
似然函数就是用结果（或样本）（9正，1负的数据）来推算参数（weight权重、概率），也就是说通过参数θ得到的预测的算法，能够尽可能地拟合样本数据（已知结果），从而最大化的使得预测结果更偏向于真实数据。
似然函数说白了就是结果导向，由已知结果来推算出预测参数θ，因为结果已经发生了，那么概率p(y|x;θ)肯定是取最大的！
最大似然估计，英文名是 maximum likelihood estimation, MLE，最大的可能性估计，这里的可能性 我理解为预测参数与样本中的x结合，使得样本结果y发生的概率
*从公式的角度理解：
我们追求的目标是预测值与实际值越接近越好，那么换句话说就是希望误差ε越小越好，甚至接近于零。
前面解释了似然函数是用数据来推算参数，通俗的说，我们用结果来计算参数值，而我们想要的结果是预测值=实际值，即ε->0,ε的取值处于0的附近；那么也就是说p(ε)的值要越大越好（前面解释过了，概率越大，ε的分布越是集中在0附近）
我们也知道，p(ε)的值和p(y|x;θ)的值是相等的，那么（p(y|x;θ)的概率也是越大越好。
那么为什么极大似然函数是一个累乘的概率积呢，因为一个单独的似然函数，概率最大时解出的θ是最满足那一个样本的参数θ，而我们的目标是要训练出一个拟合全部样本数据的θ，那么我们就不得不用累乘，来求一个联合概率密度，这个值最大时，表示 θ 使得样本集中预测值与真实值的偏差是最小的！
对数似然：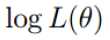
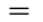
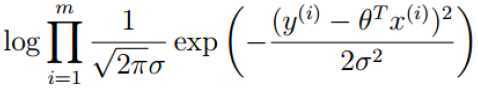
解释：乘法难解，加法就容易了，对数里面乘法可以转换成加法
展开化简：
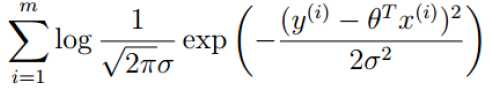
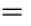
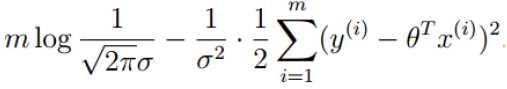
目标：让似然函数（对数变换后也一样）越大越好
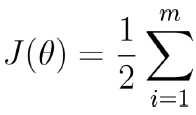
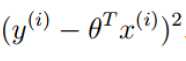（最小二乘法）
目标函数：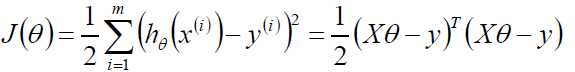
求偏导：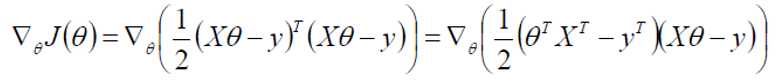
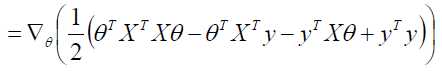
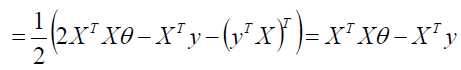
偏导等于0：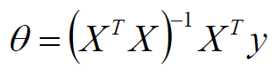
标签：和我 alt ati 概率 技术 表示 展开 等于 年龄
原文地址：https://www.cnblogs.com/lijie-blog/p/10199261.html
