标签：math   输入格式   最大值   维护   最大   连接   时空   数据   复杂度   

Ⅱ、预备知识

树链剖分，又叫重链剖分，树剖。顾名思义，就是在树上将树划分为一条条链，然后进行树上修改与查询操作(针对于结点操作，边权操作后面会讲)，用线段树来维护保证时间复杂度(数据结构模板)。一般来说，可以支持以下几种操作：
1、树上路径区间修改
2、树上路径间的区间查询(如点权之和，最大值等)
讲道理实际上线段树能做的它在树上都能做QAQ
接下来进入毒瘤内容

Ⅲ、抛出问题

先看一道板子

题目描述

如题，已知一棵包含N个结点的树（连通且无环），每个节点上包含一个数值，需要支持以下操作：
操作1：格式：1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2：格式：2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3：格式：3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4：格式：4 x 表示求以x为根节点的子树内所有节点值之和

输入输出格式

输入格式：

第一行包含4个正整数N、M、R、P，分别表示树的结点个数、操作个数、根节点序号和取模数（即所有的输出结果均对此取模）。
接下来一行包含N个非负整数，分别依次表示各个节点上初始的数值。
接下来N-1行每行包含两个整数x、y，表示点x和点y之间连有一条边（保证无环且连通）
接下来M行每行包含若干个正整数，每行表示一个操作，格式如下：
操作1： 1 x y z
操作2： 2 x y
操作3： 3 x z
操作4： 4 x

输出格式：

输出包含若干行，分别依次表示每个操作2或操作4所得的结果（对P取模）

输入输出样例

输入样例#1：

5 5 2 24
7 3 7 8 0
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3

输出样例#1：

2
21

说明：

时空限制：1s，128M
数据规模：
对于30%的数据：\(N\leq 10,M\leq 10\)
对于70%的数据：\(N\leq{10}^3,M\leq{10}^3\)
对于100%的数据：\(N\leq{10}^5,M\leq{10}^5\)
（其实，纯随机生成的树LCA+暴力是能过的，可是，你觉得可能是纯随机的么233）
样例说明：
树的结构如下：

各个操作如下：

故输出应依次为2、21(重要的事情说三遍：记得取模)

Ⅳ、分析问题

先把几个概念弄明白：

sz[u] 子树u的大小，包括u本身
dep[u] 结点u的深度，根节点深度为1
重儿子 节点u的子树中，sz最大的那个子树的根，用son[u]表示(叶结点无重儿子)
重链 由连接结点与其重儿子的边连接而成的路径(单独的结点也是一条重链)
轻链 又叫轻边，树中除了重链剩下的边
top[u] 结点u所在重链dep最小的结点(也就是最上面的点)

原谅我语文不好。。。
放张图吧QAQ

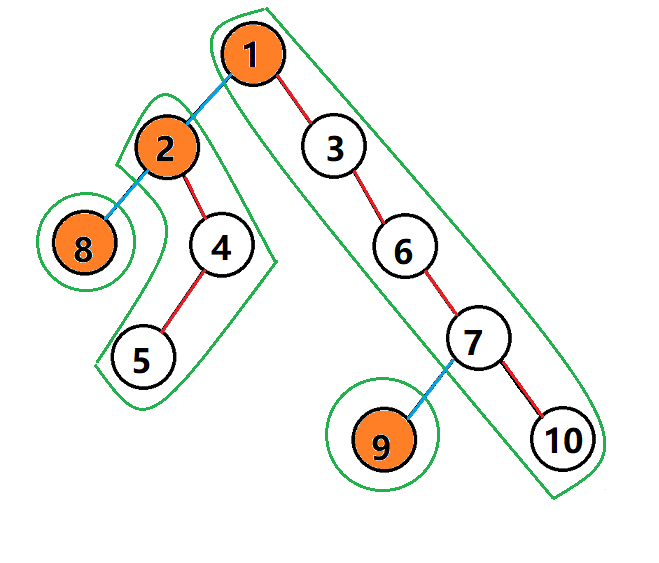
画的真帅
如图绿色框起来的是重链，橙色的是top，红的边是重链里的边，蓝的是轻边，可以发现轻边连接两条重链
举个栗子：
top[8]=8;top[7]=1;top[5]=2;son[1]=2;son[2]=8;son[6]=7;sz[2]=4;

浅谈树链剖分

标签：math   输入格式   最大值   维护   最大   连接   时空   数据   复杂度   

原文地址：https://www.cnblogs.com/hzf29721/p/10201002.html