标签:程序 dma 数据 sts nump tin 切分 读取 toc
目录
代码中涉及的数学公式可以自己下载 Typora 这款软件后,把内容复制到.md文件内通过 Typora 打开
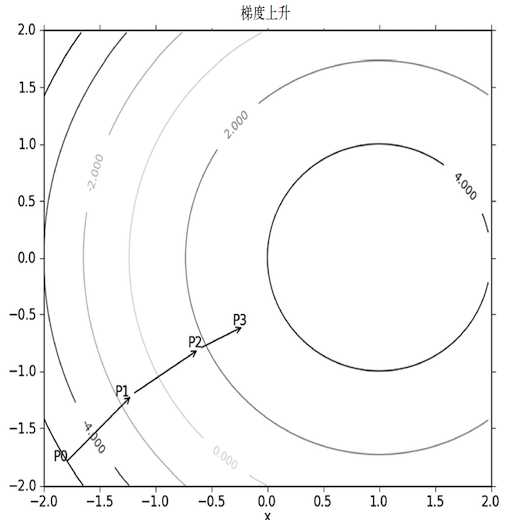
每个回归系数初始化为1
重复 R 次:
计算整个数据集的梯度
使用 alpha*gradient 更新回归系数的向量
返回回归系数
import os
import numpy as np
import matplotlib.pyplot as plt
from path_settings import machine_learning_PATH
data_set_path = os.path.join(machine_learning_PATH, '第五章/data-set')
testSet_path = os.path.join(data_set_path, 'testSet.txt')
horseColicTraining_path = os.path.join(data_set_path, 'horseColicTraining.txt')
horseColicTest_path = os.path.join(data_set_path, 'horseColicTest.txt')
def load_data_set():
"""导入数据集"""
data_mat = []
label_mat = []
# 循环导入.txt文本数据构造成列表
fr = open(testSet_path)
for line in fr.readlines():
line_arr = line.strip().split()
data_mat.append([1, float(line_arr[0]), float(line_arr[1])])
label_mat.append(int(line_arr[2]))
return data_mat, label_mat
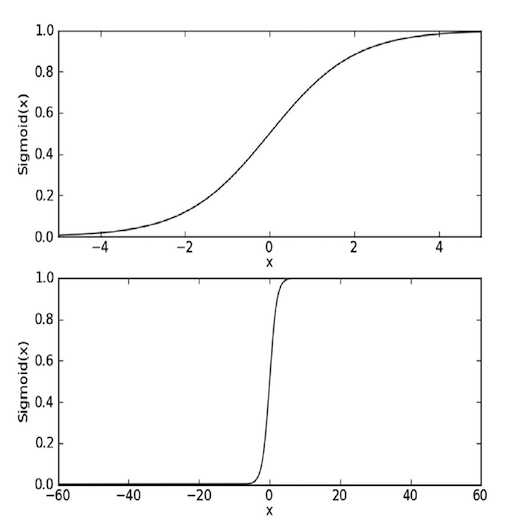
def sigmoid(in_x):
return 1 / (1 + np.exp(-in_x))
def grad_ascent(data_mat_in, class_labels):
# 生成特征矩阵
data_matrix = np.mat(data_mat_in)
# 生成标记矩阵并反置
label_mat = np.mat(class_labels).transpose()
# 计算data_matrix的行列
m, n = np.shape(data_matrix)
# 设置移动的步长为0.001
alpha = 0.001
# 设置最大递归次数500次
max_cycles = 500
# 初始化系数为1*3的元素全为1的矩阵
weights = np.ones((n, 1))
# 循环迭代梯度上升算法
for k in range(max_cycles):
# 计算真实类别与预测类别的差值
h = sigmoid(data_matrix * weights)
error = (label_mat - h)
# 调整回归系数
weights = weights + alpha * data_matrix.transpose() * error
return weights
def test_grad_ascent():
data_mat, label_mat = load_data_set()
weights = grad_ascent(data_mat, label_mat)
print(weights)
"""
[[ 4.12414349]
[ 0.48007329]
[-0.6168482 ]]
"""
if __name__ == '__main__':
test_grad_ascent()
def plot_best_fit(wei):
# getA==np.asarrayz(self)
# 使用__class__.__name__为了判断是梯度上升和随机梯度上升
if wei.__class__.__name__ == 'matrix':
weights = wei.getA()
elif wei.__class__.__name__ == 'ndarray':
weights = wei
else:
weights = wei
data_mat, label_mat = load_data_set()
# 把特征集转换成数组
data_arr = np.array(data_mat)
n = np.shape(data_arr)[0]
# 循环数据集分类
xcord1 = []
ycord1 = []
xcord2 = []
ycord2 = []
for i in range(n):
if int(label_mat[i]) == 1:
xcord1.append(data_arr[i, 1])
ycord1.append(data_arr[i, 2])
else:
xcord2.append(data_arr[i, 1])
ycord2.append(data_arr[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
# 0.1是步长
x = np.arange(-3, 3, 0.1)
# 假设 sigmoid 函数为0,并且这里的 x,y 相当于上述的 x1和x2即可得出 y 的公式
y = (-weights[0] - weights[1] * x) / weights[2]
ax.plot(x, y)
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
def test_plot_best_fit():
data_mat, label_mat = load_data_set()
weights = grad_ascent(data_mat, label_mat)
plot_best_fit(weights)
if __name__ == '__main__':
# test_grad_ascent()
test_plot_best_fit()
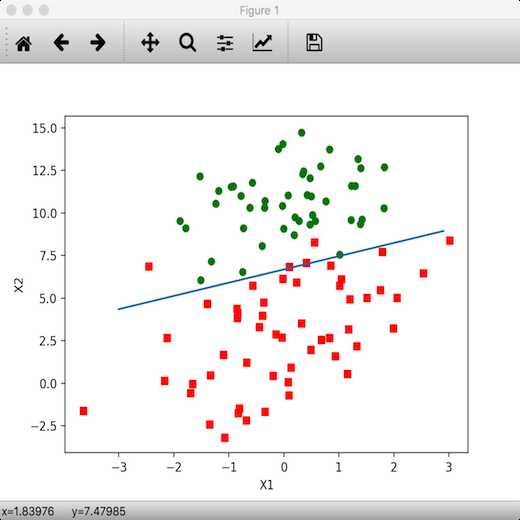
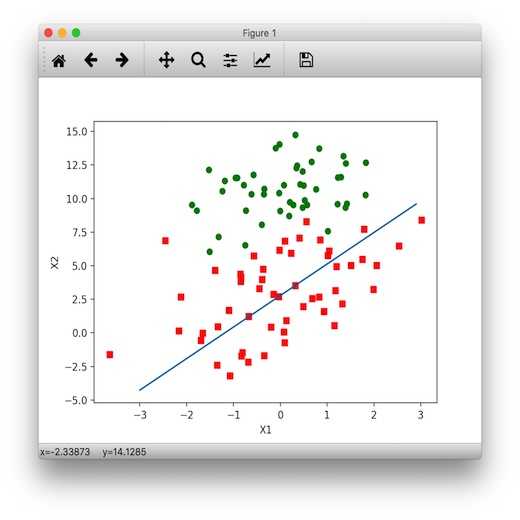
所有回归系数初始化为1
对数据集中每个样本
计算该样本的梯度
使用 alpha*gradient 更新回归系数值
返回回归系数值
def stoc_grad_ascent0(data_matrix, class_labels):
"""随机梯度上升算法"""
m, n = np.shape(data_matrix)
alpha = 0.01
weights = np.ones(n)
for i in range(m):
# 使用 sum 函数得出一个值,只用计算一次
h = sigmoid(sum(data_matrix[i] * weights))
error = class_labels[i] - h
weights = weights + alpha * error * data_matrix[i]
return weights
def test_stoc_grad_ascent0():
data_arr, label_mat = load_data_set()
weights = stoc_grad_ascent0(np.array(data_arr), label_mat)
plot_best_fit(weights)
if __name__ == '__main__':
# test_grad_ascent()
# test_plot_best_fit()
test_stoc_grad_ascent0()
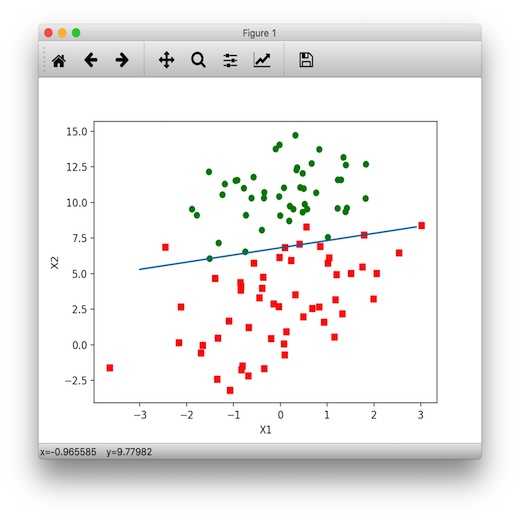
def stoc_grad_ascent1(data_matrix, class_labels, num_iter=150):
"""改进随机梯度上升算法,默认迭代150次"""
m, n = np.shape(data_matrix)
weights = np.ones(n)
for j in range(num_iter):
data_index = list(range(m))
for i in range(m):
# 每次迭代减小 alpha 的值,但最小为0.01,确保新数据依然有影响。缓解系数波动的情况
alpha = 4 / (1 + j + i) + 0.01
# 随机选取值进行更新
rand_index = int(np.random.uniform(0, len(data_index)))
h = sigmoid(sum(data_matrix[rand_index] * weights))
error = class_labels[rand_index] - h
weights = weights + alpha * error * data_matrix[rand_index]
# 删除更新后的值
del (data_index[rand_index])
return weights
def test_stoc_grad_ascent1():
data_arr, label_mat = load_data_set()
weights = stoc_grad_ascent1(np.array(data_arr), label_mat)
plot_best_fit(weights)
if __name__ == '__main__':
# test_grad_ascent()
# test_plot_best_fit()
# test_stoc_grad_ascent0()
test_stoc_grad_ascent1()
def classify_vector(in_x, weights):
prob = sigmoid(sum(in_x * weights))
if prob > 0.5:
return 1
else:
return 0
def colic_test():
"""马疝病造成马死亡概率预测"""
fr_train = open(horseColicTraining_path)
fr_test = open(horseColicTest_path)
training_set = []
training_labels = []
for line in fr_train.readlines():
# 切分所有特征并把特征加入 line_arr 列表中
curr_line = line.strip().split('\t') # type:list
line_arr = []
for i in range(21):
line_arr.append(float(curr_line[i]))
# 分开处理特征和标记
training_set.append(line_arr)
training_labels.append(float(curr_line[21]))
train_weights = stoc_grad_ascent1(np.array(training_set), training_labels, 500)
print(train_weights)
error_count = 0
num_test_vec = 0
for line in fr_test.readlines():
num_test_vec += 1
curr_line = line.strip().split('\t') # type:list
line_arr = []
for i in range(21):
line_arr.append(float(curr_line[i]))
# 通过比较样本标记与输入系数与特征相乘值 sigmoid 函数得到的标记判断是否预测失误
if int(classify_vector(np.array(line_arr), train_weights)) != int(curr_line[21]):
error_count += 1
error_rate = (float(error_count) / num_test_vec)
print('测试集的错误率: {}'.format(error_rate))
# 测试集的错误率: 0.373134328358209
return error_rate
def multi_test():
num_tests = 10
error_sum = 0
for k in range(num_tests):
error_sum += colic_test()
print('迭代 {} 次后平均错误率为: {}'.format(num_tests, error_sum / float(num_tests)))
# 迭代 10 次后平均错误率为: 0.3656716417910448
if __name__ == '__main__':
# test_grad_ascent()
# test_plot_best_fit()
# test_stoc_grad_ascent0()
# test_stoc_grad_ascent1()
multi_test()
import os
import numpy as np
import matplotlib.pyplot as plt
from path_settings import machine_learning_PATH
data_set_path = os.path.join(machine_learning_PATH, '第五章/data-set')
testSet_path = os.path.join(data_set_path, 'testSet.txt')
horseColicTraining_path = os.path.join(data_set_path, 'horseColicTraining.txt')
horseColicTest_path = os.path.join(data_set_path, 'horseColicTest.txt')
def load_data_set():
"""导入数据集"""
data_mat = []
label_mat = []
# 循环导入.txt文本数据构造成列表
fr = open(testSet_path)
for line in fr.readlines():
line_arr = line.strip().split()
data_mat.append([1, float(line_arr[0]), float(line_arr[1])])
label_mat.append(int(line_arr[2]))
return data_mat, label_mat
def sigmoid(in_x):
"""构造 sigmoid 函数"""
return 1 / (1 + np.exp(-in_x))
def grad_ascent(data_mat_in, class_labels):
"""梯度上升算法"""
# 生成特征矩阵
data_matrix = np.mat(data_mat_in)
# 生成标记矩阵并反置
label_mat = np.mat(class_labels).transpose()
# 计算data_matrix的行列
m, n = np.shape(data_matrix)
# 设置移动的步长为0.001
alpha = 0.001
# 设置最大递归次数500次
max_cycles = 500
# 初始化系数为1*3的元素全为1的矩阵
weights = np.ones((n, 1))
# 循环迭代梯度上升算法
for k in range(max_cycles):
# 计算真实类别与预测类别的差值
h = sigmoid(data_matrix * weights)
error = (label_mat - h)
# 调整回归系数
weights = weights + alpha * data_matrix.transpose() * error
return weights
def test_grad_ascent():
data_mat, label_mat = load_data_set()
weights = grad_ascent(data_mat, label_mat)
print(weights)
"""
[[ 4.12414349]
[ 0.48007329]
[-0.6168482 ]]
"""
def plot_best_fit(wei):
"""画出被分割的数据集"""
# getA==np.asarrayz(self)
# 使用__class__.__name__为了判断是梯度上升和随机梯度上升
if wei.__class__.__name__ == 'matrix':
weights = wei.getA()
elif wei.__class__.__name__ == 'ndarray':
weights = wei
else:
weights = wei
data_mat, label_mat = load_data_set()
# 把特征集转换成数组
data_arr = np.array(data_mat)
n = np.shape(data_arr)[0]
# 循环数据集分类
xcord1 = []
ycord1 = []
xcord2 = []
ycord2 = []
for i in range(n):
if int(label_mat[i]) == 1:
xcord1.append(data_arr[i, 1])
ycord1.append(data_arr[i, 2])
else:
xcord2.append(data_arr[i, 1])
ycord2.append(data_arr[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
# 0.1是步长
x = np.arange(-3, 3, 0.1)
# 假设 sigmoid 函数为0,并且这里的 x,y 相当于上述的 x1和x2即可得出 y 的公式
y = (-weights[0] - weights[1] * x) / weights[2]
ax.plot(x, y)
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
def test_plot_best_fit():
data_mat, label_mat = load_data_set()
weights = grad_ascent(data_mat, label_mat)
plot_best_fit(weights)
def stoc_grad_ascent0(data_matrix, class_labels):
"""随机梯度上升算法"""
m, n = np.shape(data_matrix)
alpha = 0.01
weights = np.ones(n)
for i in range(m):
# 使用 sum 函数得出一个值,只用计算一次
h = sigmoid(sum(data_matrix[i] * weights))
error = class_labels[i] - h
weights = weights + alpha * error * data_matrix[i]
return weights
def test_stoc_grad_ascent0():
data_arr, label_mat = load_data_set()
weights = stoc_grad_ascent0(np.array(data_arr), label_mat)
plot_best_fit(weights)
def stoc_grad_ascent1(data_matrix, class_labels, num_iter=150):
"""改进随机梯度上升算法,默认迭代150次"""
m, n = np.shape(data_matrix)
weights = np.ones(n)
for j in range(num_iter):
data_index = list(range(m))
for i in range(m):
# 每次迭代减小 alpha 的值,但最小为0.01,确保新数据依然有影响。缓解系数波动的情况
alpha = 4 / (1 + j + i) + 0.01
# 随机选取值进行更新
rand_index = int(np.random.uniform(0, len(data_index)))
h = sigmoid(sum(data_matrix[rand_index] * weights))
error = class_labels[rand_index] - h
weights = weights + alpha * error * data_matrix[rand_index]
# 删除更新后的值
del (data_index[rand_index])
return weights
def test_stoc_grad_ascent1():
data_arr, label_mat = load_data_set()
weights = stoc_grad_ascent1(np.array(data_arr), label_mat)
plot_best_fit(weights)
def classify_vector(in_x, weights):
prob = sigmoid(sum(in_x * weights))
if prob > 0.5:
return 1
else:
return 0
def colic_test():
"""马疝病造成马死亡概率预测"""
fr_train = open(horseColicTraining_path)
fr_test = open(horseColicTest_path)
training_set = []
training_labels = []
for line in fr_train.readlines():
# 切分所有特征并把特征加入 line_arr 列表中
curr_line = line.strip().split('\t') # type:list
line_arr = []
for i in range(21):
line_arr.append(float(curr_line[i]))
# 分开处理特征和标记
training_set.append(line_arr)
training_labels.append(float(curr_line[21]))
train_weights = stoc_grad_ascent1(np.array(training_set), training_labels, 500)
print(train_weights)
error_count = 0
num_test_vec = 0
for line in fr_test.readlines():
num_test_vec += 1
curr_line = line.strip().split('\t') # type:list
line_arr = []
for i in range(21):
line_arr.append(float(curr_line[i]))
# 通过比较样本标记与输入系数与特征相乘值 sigmoid 函数得到的标记判断是否预测失误
if int(classify_vector(np.array(line_arr), train_weights)) != int(curr_line[21]):
error_count += 1
error_rate = (float(error_count) / num_test_vec)
print('测试集的错误率: {}'.format(error_rate))
# 测试集的错误率: 0.373134328358209
return error_rate
def multi_test():
num_tests = 10
error_sum = 0
for k in range(num_tests):
error_sum += colic_test()
print('迭代 {} 次后平均错误率为: {}'.format(num_tests, error_sum / float(num_tests)))
# 迭代 10 次后平均错误率为: 0.3656716417910448
if __name__ == '__main__':
# test_grad_ascent()
# test_plot_best_fit()
# test_stoc_grad_ascent0()
# test_stoc_grad_ascent1()
multi_test()
==尊重原创==
==可以伸出你的小手点个关注,谢谢!==
博客园地址:https://www.cnblogs.com/chenyoude/
git 地址:https://github.com/nickcyd/machine_learning
微信:a1171958281
标签:程序 dma 数据 sts nump tin 切分 读取 toc
原文地址:https://www.cnblogs.com/chenyoude/p/10201778.html