2D射影几何和变换

标签：ogr   就是   需要   lin   的区别   二维   sha   图片   tps   

阅读《计算机视觉中的多视图集合》

2D射影几何和变换

2D射影平面

本章的关键是理解线和点的对偶性。从射影平面模型出发，IP^2^内的点(a, b ,c)由IP^3^空间中一条过原点的射线k(x1, x2, x3)^T^表示。点采用的是齐次坐标表示，具有相同比例，不同缩放因子的表示都是同一个点，就像射线也可以用同比例，不同缩放因子的向量表示一样。

射影变换projectivity

• 射影映射，也叫保线变换，或者射影变换，或者单应(homography)，都是同义词，其性质是保线性，即直线变换之后还是直线。 可以用一个8自由度的三维非奇异矩阵H表示。
• 只需要4个任意三点不共线的点即可以求得射影变换H，然后求得逆矩阵H^-1^即可以消除射影变换H带来的变化。
• 透视变换，也即中心投影，是射影变换的一种，它的特点是：连接对应的直线共点。透视变换的复合不再是透视变换，但还会是射影变换。

• 如果有一个射影变换H，点x变换之后为Hx，那么在同样的变换下，直线I变换为H^-T^I。我们称点的变换为逆变，线的变换为协变。

  变换的层次

  如下表，下层的都是上层变化的特例。
  
  另外还有一个透视变换perspectivity，它是射影变换的一个特例，与仿射变换affine的区别：

1. 透视变换可以用于把3D变成2D，而仿射变换都是2D平面
2. 透视变换可以有切变shareing
3. 仿射变换的右下角必须为1，而透视不会
4. 如果是两个平面的投射，且都是Euclidean坐标，那么透视变换也只有6个自由度

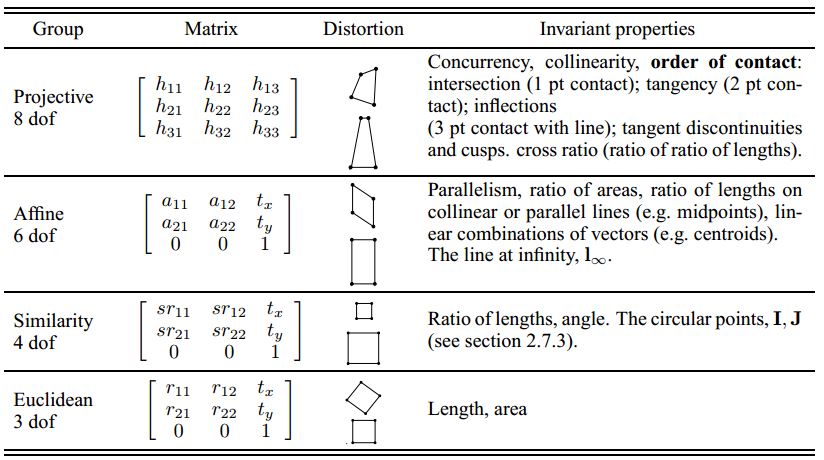
透视变换与射影变换的区别：

1. 多个透视变换的组合还会是射影变换，但一般不会是透视变换
2. 透视变换中，连接原始点和透视点的所有连线交于一点，这也即是中心投影的含义。

从图线恢复仿射和度量性质

重要概念

• 理想点：在齐次表示法中，最后坐标为0，比如二维坐标中的\(x_3=0\),的点即为理想点，也即无穷远点,通用表达为\((x_1, x_2, 0)^T\)
• 无穷远线：用符号\(I_{\infty}\)表示，\(I_{\infty}=(0,0,1)^T\),显然，\((0,0,1)(x_1, x_2, 0)^T=0\)，即理想点和无穷远线相交
• 消影线：无穷远线被影像到像平面的直线
• 虚圆点：在\(I_{\infty}\)上有两个不动点\(I=(1,i,0)\)和\(J=(1,-i,0)\),这两个点是不动点的冲要条件为相似变换，\(I‘=H_SI=I\),\(J‘=H_SJ=J\)，\(H_S\)表示相似变换矩阵， 即经过相似变换，他们的坐标不变。

• 与虚圆点对偶的二次曲线：记为\(C^*_{\infty}\)，\(C^*_{\infty}=IJ^T+JI^T=\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0\\ 0& 0 & 0 \end{bmatrix}\)。同理，根据对偶定理，二次曲线\(C^*_{\infty}\)为不动曲线的冲要条件为变换为相似变换。

  直接从透视图像恢复

  对应的书本中的例 1.26。

1. 假设有任意射影变换H
2. 根据书中结论1.23，找到五组世界平面中相互正交的直线对，找到他们在变换之后的图像中的对应像直线，即可以求得经过变换H之后的\(C^*_{\infty}\)的像\(C^{*‘}_{\infty}\)

3. 根据结论1.24，对\(C^{*‘}_{\infty}\)进行SVD分解，即可得到一个变换U，用这个U对像进行校正，就会得到一个与H变换之前只相差一个相似变换的结果。这样我们就可以根据相似变换的不动量特性来测量某些数据。

   分层法恢复

4. 在世界平面中平行的两组平行线，找到他们在像中的对应线，然后找到他们的交点，两组平行线就会有两组交点，根据平行线交于无穷远点的理论，这两个交点的连线就是消影线。然后根据公式1.18就可以得到一个变换H，可以把像变换到和世界平面只差一个仿射变换

5. 在已经只存在仿射变换的图像中，找到两对在世界平面中正交的直线的像，然后根据结论1.23就可以求出仿射变换矩阵K。这个K把一个与世界平面只差一个相似变换的平面变换到当前仿射变换图像。

2D射影几何和变换

标签：ogr   就是   需要   lin   的区别   二维   sha   图片   tps   

原文地址：https://www.cnblogs.com/willhua/p/10201962.html