标签：one   定义   偶数   三角函数   tar   back   图像   mic   img   

基本初等函数

本文主要记载五种基本初等函数。

目录

概述

幂函数

指数函数

对数函数

三角函数

反三角函数

概述

基本初等函数，包括了幂函数、指数函数、对数函数、三角函数和反三角函数五种。由这些基本初等函数经过有限次的四则运算（加减乘除）和函数的复合所得到的函数称为初等函数。

幂函数 power function

公式

$y=x^\alpha$

其中，$x$是自变量，$\alpha$是常数。

图像和性质

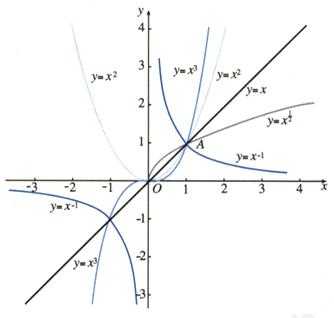
 （1）所有幂函数的图像都过$(1,1)$点。

（2）当$\alpha$为奇数时，幂函数为奇函数；当$\alpha$为偶数时，幂函数为偶函数。

（3）考虑幂函数在第一象限中的特征，当$\alpha>0$时，幂函数在$(0,+\infty)$上为增函数；当$\alpha<0$时，幂函数在$(0,+\infty)$上为减函数。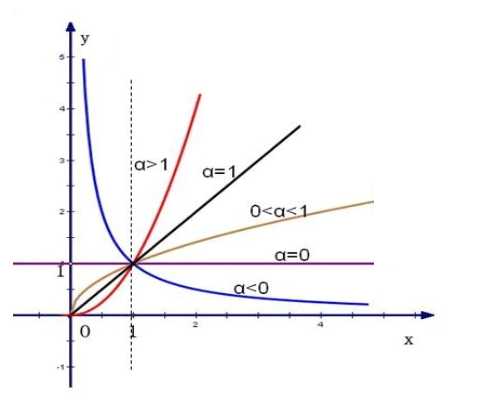

指数函数 exponential function

公式

$y=a^x (a>0, a \neq 1)$

图像和性质

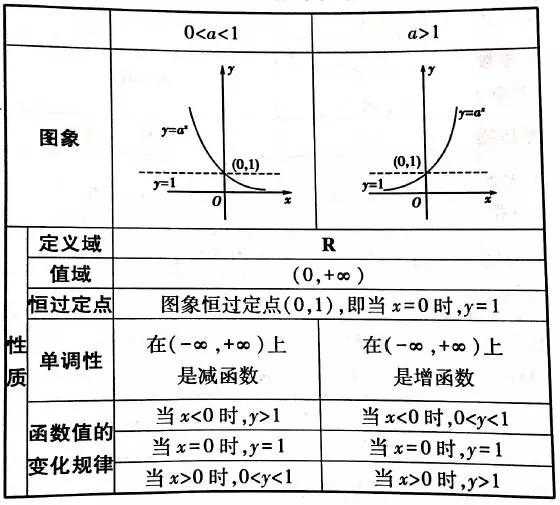
（1）所有的指数函数都过点$(0,1)$，定义域为$R$，值域为$(0,+\infty)$

运算

$a^ra^s=a^{r+s}$

$(a^r)^s=a^{rs}$

$(ab)^r=a^rb^r$

$a^{\frac{m}{n}}=\sqrt[n]{a^m}$

幂函数和指数函数的对比

幂函数   $y=x^\alpha$   $x$为底数

指数函数 $y=a^x$ $x$为指数

对数函数 logarthmic function

公式

$y=log_a x$

图像和性质

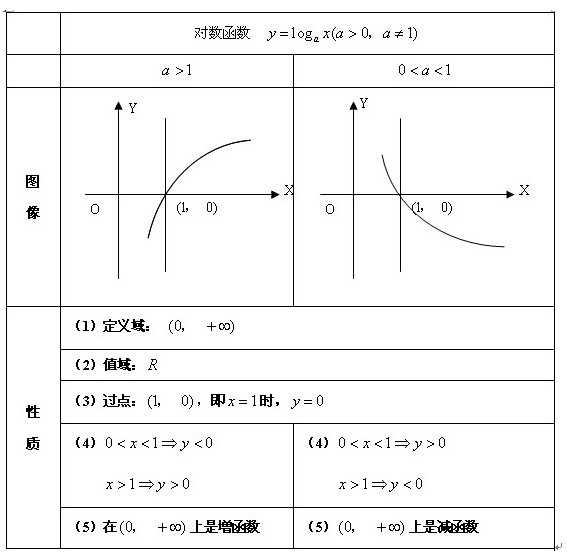
（1）所有对数函数都过点$(1,0)$

运算

$a^b=N \leftrightarrow b=log_a N$

$a^{log_a N}=N$

$log_a b=\frac{log_c b}{log_c a}$

$log_a b=\frac{1}{log_b a}$

$log_a b*log_b c=log_a c$

$log_{a^m} {b^n}=\frac{n}{m}log_a b (m \neq 0)$

$log_a {MN}=log_a M+log_a N$

$log_a {\frac{M}{N}}=log_a M-log_a N$

$log_a {M^n}=n*log_a M$

增长趋势的比较

随着x的增加，指数函数爆炸增长，幂函数逐渐增长，对数函数缓慢增长。

三角函数

反三角函数

基础数学：基本初等函数

标签：one   定义   偶数   三角函数   tar   back   图像   mic   img   

原文地址：https://www.cnblogs.com/liuyingsme/p/10201678.html