标签:分享图片 定义 图片 2.x 前缀和 完全二叉树 深度 数列 log
未知出处
题意:
定义一个无穷长的数列,满足以下性质:
$1.X_{2n}=-{X_{n}}$
$2.X_{2n}=(-1)^{(n+1)}*X_{n}$
$3.X_{2n-1}=(-1)^{(n+1)}*X_n$
1e5个询问,求:
$1.X_k$
$2.S_k$即前缀和
(大概是这样)
画一画递推式的图,或者观察2n,n可以看到转移类似一个二叉树。
第一个点要特判
树高logn
左右儿子有不同的边权
可以类似二进制差分,一路走到$X_k$即可求出第一问
第二问,
发现是一个连续的子树块
往1点走,发现可以把两边的子树分别算上,而且都是完全二叉树!
可以dp[deep][0/1][0/1]表示深度为deep的完全二叉树的根节点权值-1/+1,奇偶性0/1时,子树的和(这个是固定的)
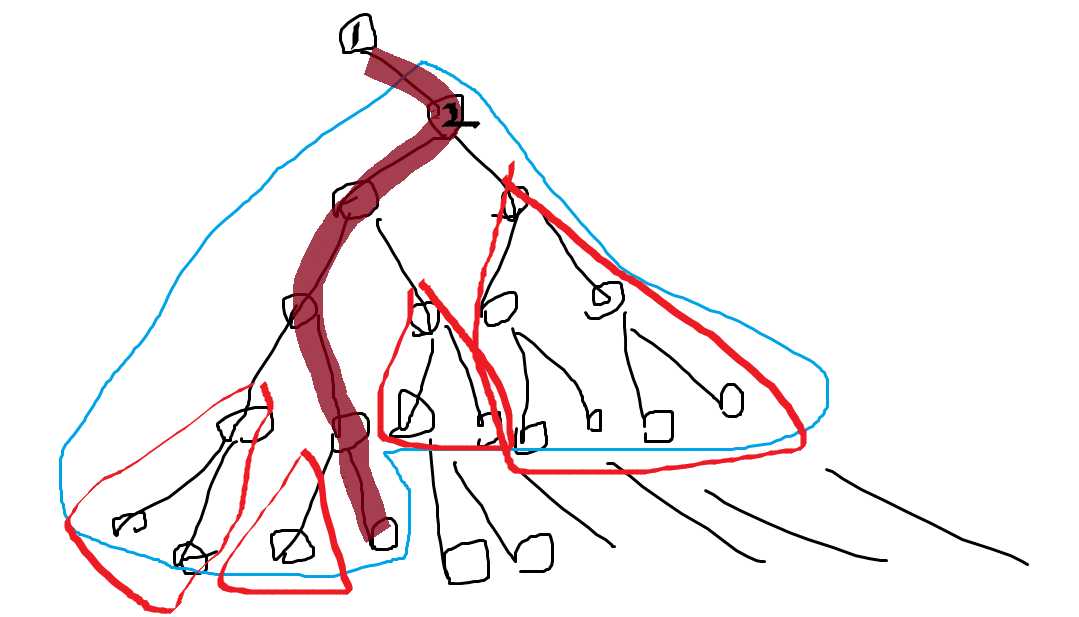
logn走一下即可。
特判1点
标签:分享图片 定义 图片 2.x 前缀和 完全二叉树 深度 数列 log
原文地址:https://www.cnblogs.com/Miracevin/p/10202547.html