标签:自变量 正弦 img 集合 不同 图形 大于 关于 高等数学
一、映射
设X,Y是两个非空集合,如果存在一个法则f
·使得对x中每个元素x 按法则f
·在Y中有唯一确定的元素y与之对应,
·则称f为从X到Y的映射 记作f:X->Y
·元素y称为元素x的像,元素x称为元素y的一个原像
举例:照镜子 镜子中也有一个你 (像和原像
·定义域:集合X称为映射f的定义域 记作Df 即Df=X
·值域:X中所有元素的像组成的集合称为映射f的值域
记作Rf或f(X) 即:
Rf = f(X) = {f(x)|x∈X}
映射三要素
·集合X 即定义域Df=X
·集合Y 即值域的范围 Rf?Y (Y不是值域,Y包含Rf)
·对应法则f 使对每个x∈X 有唯一确定的y=f(x)与之对应
注意
·对每个x∈X 元素x的像y是唯一的
·对每个y∈Rf 元素y的原像不一定是唯一的
·映射f的值域Rf是Y的一个字集 即Rf?Y 不一定Rf=Y
·满射 Rf=Y
·单射 任意x1 x2 ∈X x1≠x2 有f(x1)≠f(x2)
·一一映射:满射+单射
·函数的概念
函数的定义(function)
·设数集D?R(实数集) 则称映射f:D->R为定义在D上的函数 通常简记为y=f(x) x∈D
·其中x称为自变量,y称为因变量 D称为定义域 记作Df 即Df=D
·函数值:对每个x∈D 按对应法则f 总有唯一确定的值y与之对应 这个值称为函数f在x处的函数值 记作f(x)
·函数关系:因变量y与自变量x之间的这种依赖关系称为函数关系
·值域:函数值f(x)全体构成的集合称为函数f的值域 记作Rf或f(D)
函数的两要素
·定义域与对应法则
函数的定义域
·有实际意义背景的函数 根据实际背景中变量的实际意义确定
例:自由落体运动 s= 1/gt^2 t∈[0,T]
·抽象的用算式表达的函数 其定义域是自变量所能取的使算式有意义的一切实数值
y= D:[-1,1]
y= (分母不能为0 根号内也要大于0 所以使(-1,1)
函数的图形表示方法
·坐标平面上的点集{P(x,y)|y=f(x),x∈D},称为函数y=f(x) x∈D的图形
特殊函数举例:
·符号函数
·y=sgnx = {1(当x>0 0(当x=0 -1(当x<0
(想象一下它的图形)
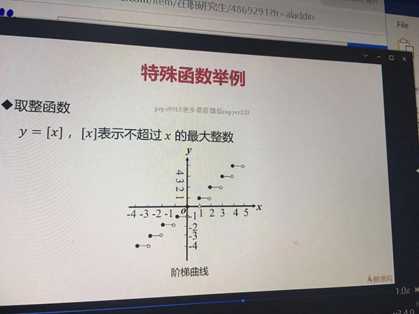
·取整函数
y=[x],[x]表示不超过x的最大整数
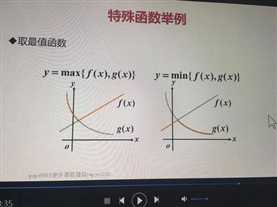
·取最值函数
y=max{f(x),g(x)}
·分段函数
·在自变量的不同变化范围中,对应法则用不同的式子来表示的函数,称为分段函数
三、函数的特性
函数的有界性
·若X?D 存在M>0 对任意x∈X 有|f(x)|<=M成立 则成f(x)在X上有界,否则称无界
函数的单调增加性
·设函数f(x)的定义域为D 区间I?D
·如果对于区间I上任意两点x1及x2
·当x1<x2 恒有f(x1)<f(x2)
则称f(x)在区间I上是单调增加的
函数的单调减少性
…
函数的奇偶性
·设D关于原点对称
·对于任意x∈D 有f(-x)=f(x)
则称函数f(x)为偶函数
·设D关于原点对称,
·对于任意x∈D 有f(-x)=-f(x)
则称函数f(x)为奇函数
函数的周期性
·设函数f(x)的定义域为D 如果存在一个不为零的数l 使得对于任一x∈D (x+-l)∈D 且f(x+l)=f(x)恒成立,则称f(x)为周期函数,l称为f(x)的函数

四、初等函数
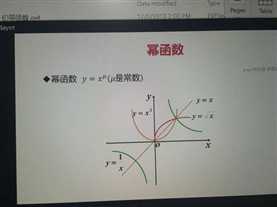
·幂函数 y=x^u
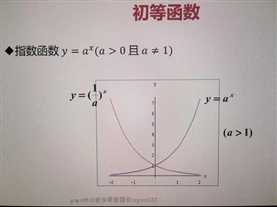
·指数函数 y=a^x
·对数函数 y = logax (a>0且a≠1)
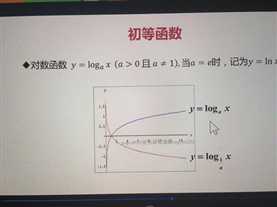
1) 当a=e时 记为y=lnx
·三角函数
·正弦函数 y = sinx
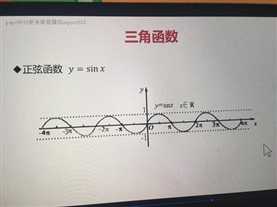
·余弦函数 y = cosx
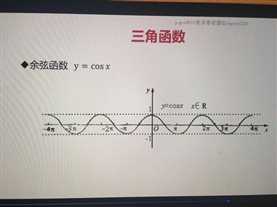
·正切函数 y = tanx
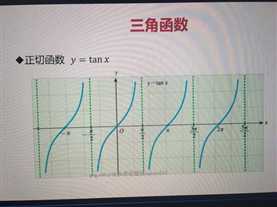
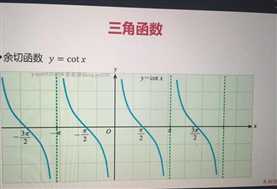
·余切函数 y = cotx
标签:自变量 正弦 img 集合 不同 图形 大于 关于 高等数学
原文地址:https://www.cnblogs.com/eret9616/p/10204846.html