标签:假设 level 健康 ref 学习 比较 注意 基于 再计算
P(A∩B)和P(A|B)有什么区别?
这个问题困惑了我这么多年,是最近半年才发现的。前者注意,基数是全部样本数量,后者是B
P(A∩B) = AB同时满足的个数/ Num(total)
P(A | B) =AB同时满足的个数/ Num(B)
二者分子是一样的,区别在于分母。
贝叶斯是什么思想?
P(h|D) = P(D|h)P(h)/P(D),这里P(D|h)代表广义上面的已知的概率,即先验概率;比如病症并判,患者成化验呈POS的概率=>P(POS|h);这个是先验的,什么叫先验?已经验证了的,即:基于结论,条件的概率,广而告之的,那么现在翻转一下,一个具体的患者,化验呈POS,那么他是患者的概率都大?问题=>P(h|POS),变成了后验概率了,什么是后验,后验就是基于条件,结论满足的概率多大?对于具体化的场景下,如何利用先验概率求得后验概率就是贝叶斯公式解决的问题。
比如Jenny是女性,多少概率在Havard念书;Harvard女性概率是47%,那个47%的概率是先验,结论是harvard念书,条件是女性;但是这个P(D|h)直接拿来对于Jenny并没有多少用;现在Jenny关心的她在Harvard概率多大,那么其实问题是Jenny作为一个女性,在Harvard的概率是多大?这个是后验概率;女性是条件,作为基数,结论的概率多大?
贝叶斯在使用的时候更多的时候是用在概率比较上,如果基数P(h)都一致,不必要再计算除以P(D)取值,那么其实比较P(D|h)P(h)即可。
机器学习的时候,我们通常会面对一个问题,样本以及属性的处理,记住如果用向量来表达样本,那么横向是样本(由各个属性组成),那么我们分析的方向是纵向,对于各个样本的属性的分布进行学习和分析;这个是机器学习的一个模式,就是分析同类样本(指的是监督学习)各个样本某个属性的分布;推出一些分布规律,然后多个属性的分布组合在一起形成一个属性簇的分布;这样就可以作为整个分类的一个模型;然后,拿来一个样本就用这个模型来分析这个样本(向量)是这个分类的概率是多大。
比如例子:
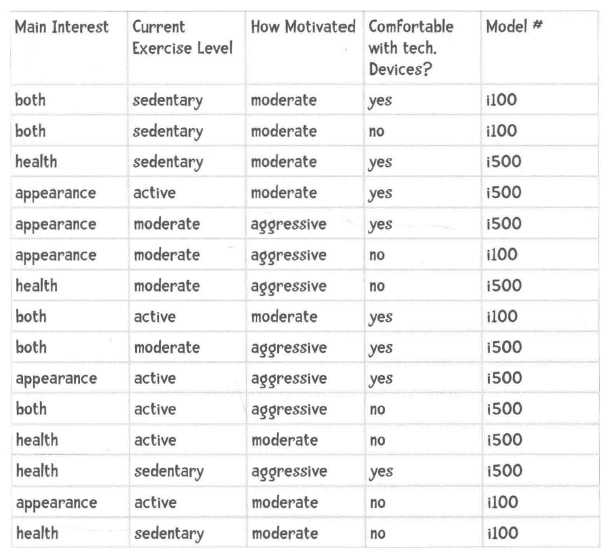
横向是向量,那么我们分析的方向就是纵向的属性的分布,比如我们可以通过这些数据获知最终买了i100的用户中等运动的人概率多少(Exercise Level)=>P(中等运动|i100),买i100的目的是健康/美丽的比重是多少=>P(美丽|i100)或者P(健康|i100),买i100的动机强烈/中等有多少等等,我们分析的目标其实是针对一个属性的。在通过贝叶斯公式进行计算的时候,分布都是P(i100)即购买i100占比,值是一样的;所以我们在计算
那么贝叶斯的精华来了,小明是为了健康,运动强度中等...那么小明买i100的概率多大,买i150的概率多大?这里上述列表提炼出来的买i100的人群中,属性的分布(概率)情况就是先验概率,那么后验的明显和先验情况相反,那么我们需要求得就是就先验概率来推断出后验概率。
P(i100|健康&中等强度&....)=P(健康|i100) * p(运动强度中等|i100) * P(...|i100) * P(i100)=a
P(i1500|健康&中等强度&....)=P(健康|i500) * p(运动强度中等|i500)* P(...|i500) * P(i500)=b
下面比较的就是a和b的大小,那么根据结果就是给小明推荐i100还是i500了。注意上述公式一和公式二分母都是P(健康&中等强度&....)所以可以忽略,比较分子的值即可。
分析这类问题其实可以不用这么烧脑,分析完题意之后,直接写下P(i100|健康&中等强度&....),那么倒逼的就是要求解P(健康|i100),P(中等强度|i100)...即可。
没完,这种方式看似无公害,但是在小样本场景下,如果某个属性分布为0,那么将会导致求得a/b是0,是0就不合理了,任何属性都是存在的可能性。于是另外一个公式横空出世了:
P(x|y)=(nc + mp)/ (n + m)
之前:
p(x|y)=nc/n
那么新公式里面的mp都是什么意思,m代表属性取值的个数,比如Exercise Level有三个,m=3,p代表各个属性的概率,这个概率是指每个属性出现的概率,默认情况是机会均等(并不是样本中出现的概率),所mp很多时候都是1,新公式很好的解决了0问题,这样计算出来的概率就不会因为某一项为0而导致彻底凉凉。
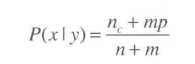
上面的例子中,属性都是离散分布,如果是连续分布怎么办?第一种办法是将连续数据进行分类,比如100-1000代表中等,1000-5000代表高等。。。将连续的数据分段划分;第二种方法就是默认属性的分布式正态分布,通过高斯函数进行求解。
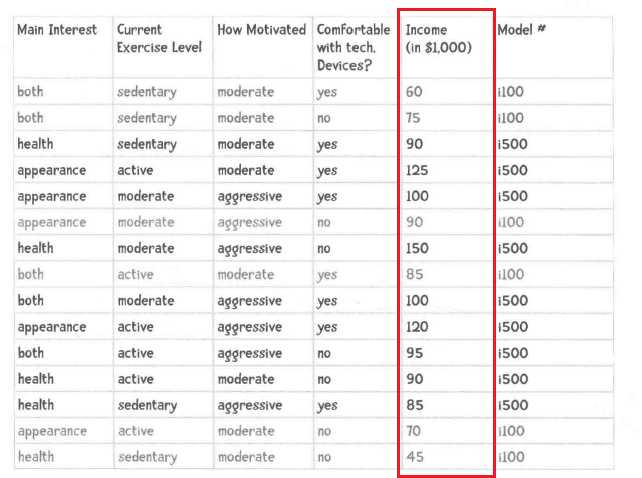
计算一下这个属性的样本标准差以及均值,带入到下面的公式中,将入我们想要知道收入为100000(100K)的比重是多少:
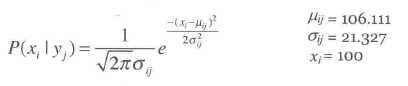
可以求得均值,可以求出样本标准差,设置xi为目标100K带入到公式中即可算的概率。
是不是正态分布可以通过QQplot等方式来进行论证,这里公式我理解并不限于正态分布,可以是t分布,可以是F分布,需要提前验证一下。
对于正态分布,他会满足一条件,就是68%的数据都是会落在一个标准差范围内,95%的数据将会落在2个标准差范围内;这里还有一个概念,就是方差和标准差,标准差里面有总体标准差和样本标准差。
方差是样本特征和特征均值之差;总体标准差则是方差均值开根号:

还有一个样本标准差:
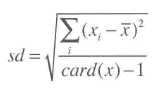
样本标准差一般认为是比总体标准差更好地估计。
那么为什么叫朴素贝叶斯呢?因为我们在计算的时候,都会建立一个假设,贝叶斯公式中牵涉的属性之间是没有关联性(但是实际情况大多数并非如此),所以我们在计算概率的时候可以毫不犹豫的把各个属性的概率直接做乘法,因为这个假设将贝叶斯的使用场景极大简化,所以称之为朴素贝叶斯,但是即使我们假设为无关联,其实效果来还是不错的。
参考:
写给程序员的数据挖掘
标签:假设 level 健康 ref 学习 比较 注意 基于 再计算
原文地址:https://www.cnblogs.com/xiashiwendao/p/10205427.html