【[POI2014]HOT-Hotels】

标签：个数   char   pre   for   getc   math   lin   down   代码   

魏佬怒嘲我只会做给定一棵树，输出有多少个点这种问题

不过我连这个也不会做

还算一道不错的树上数数题目

但是我一直不会数数

求树上所有的三元组\((u,v,t)\)，满足\(dis(u,v)=dis(u,t)=dis(v,t)\)的个数

感觉好神仙啊，一眼不会的感觉

之后试着挖掘一下性质，发现只要我们需要找一个点\(x\)使得这三个点到\(dis(x,u)=dis(x,v)=dis(x,t)\)好像就可以了

吗？

显然不行啊

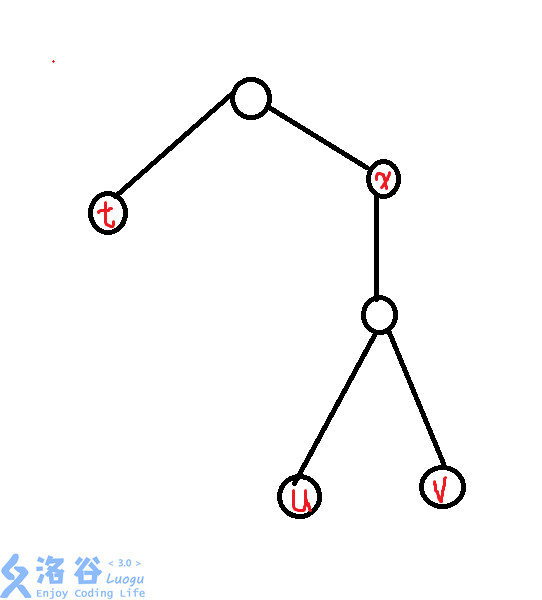
就比如这一棵树，确实这里是有\(dis(x,u)=dis(v,x)=dis(t,x)=2\)，但是\(dis(u,v)=2\)，而\(dis(t,u)=4\)，这显然并不对

所以这个性质还得有一个限制条件，就是\(x=LCA(u,v)\)

我们把问题分成两步

1. \(u,v,t\)在一棵子树里

2. \(u,v\)在一棵子树里，\(t\)在子树外

有没有\(up\ and\ down\)的意味了，在\(up\)里我们就能统计第一种情况的答案了

我们定义\(dp[x][j]\)表示在\(x\)的子树内部有多少个点到达\(x\)的距离为\(j\)，显然这个非常好转移

\(f[x][j]\)表示在\(x\)的子树内部，有多少对\((u,v)\)满足\(dis(u,v)=j\)，且\(LCA(u,v)=x\)，这个在合并子树的时候也可顺边求出来

而合并子树的时候，我们每次合并的时候就可以统计第一种答案了，由于\(u\)和\(v\)显然不能来自于同一棵子树内部，所以合并的时候直接拿这个去乘上之前的\(f[x][j]\)就好了

第二种情况，我们直接\(down\)下来，首先还是先\(down\)一下\(dp\)数组，求出子树外部到\(x\)距离为\(j\)的点有多少个，这些点就可以作为\(t\)，之后乘上\((u,v)\)点对的数量，我们就可以把答案合并出来了

代码

#include<iostream>
#include<cstring>
#include<cstdio>
#define re register
#define maxn 5001
#define LL long long
#define max(a,b) ((a)>(b)?(a):(b))
struct E
{
    short v,nxt;
}e[maxn<<1];
short deep[maxn],head[maxn],md[maxn];
int dp[maxn][maxn],f[maxn][maxn];
int n,num;
LL ans;
inline void add_edge(int x,int y)
{
    e[++num].v=y;
    e[num].nxt=head[x];
    head[x]=num;
}
inline int read()
{
    char c=getchar();
    int x=0;
    while(c<‘0‘||c>‘9‘) c=getchar();
    while(c>=‘0‘&&c<=‘9‘)
        x=(x<<3)+(x<<1)+c-48,c=getchar();
    return x;
}
inline LL merge(LL x,LL y)
{
    return (x-1)*x/2*y;
}
void dfs(int x)
{
    dp[x][0]++;
    for(re int i=head[x];i;i=e[i].nxt)
    if(!deep[e[i].v])
    {
        md[e[i].v]=deep[e[i].v]=deep[x]+1;
        dfs(e[i].v);
        md[x]=max(md[x],md[e[i].v]);
        for(re int j=1;j<=md[x];j++)
            ans+=f[x][j]*dp[e[i].v][j-1],f[x][j]+=dp[x][j]*dp[e[i].v][j-1],dp[x][j]+=dp[e[i].v][j-1];
    }
}
void Redfs(int x)
{
    for(re int i=head[x];i;i=e[i].nxt)
    if(deep[e[i].v]>deep[x])
    {
        for(re int j=n;j;j--)
            if(j>=2) ans+=(dp[x][j-1]-dp[e[i].v][j-2])*f[e[i].v][j],dp[e[i].v][j]+=dp[x][j-1]-dp[e[i].v][j-2];
                else ans+=dp[x][j-1]*f[e[i].v][j],dp[e[i].v][j]+=dp[x][j-1];
        Redfs(e[i].v);
    }
}
int main()
{
    n=read();
    int x,y;
    for(re int i=1;i<n;i++)
        x=read(),y=read(),add_edge(x,y),add_edge(y,x);
    md[1]=deep[1]=1;
    dfs(1);
    Redfs(1);
    std::cout<<ans;
    return 0;
}

【[POI2014]HOT-Hotels】

标签：个数   char   pre   for   getc   math   lin   down   代码   

原文地址：https://www.cnblogs.com/asuldb/p/10205774.html