标签:大小 排序 进制 更新 长度 结构 不容易 code 问题
一、概念
1.定义
是一种树形结构,是一种哈希树的变种,又名单词查找树。
2.基本性质
(1)根节点不包含字符,除根节点外每一个节点都只包含一个字符。
(2)从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
(3)每个节点的所有子节点包含的字符都不相同。
4.优点
擅于处理前缀问题,比hash查询快。
5.缺点
占空间大,易爆内存。
3.应用
典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串)。
二、实现过程
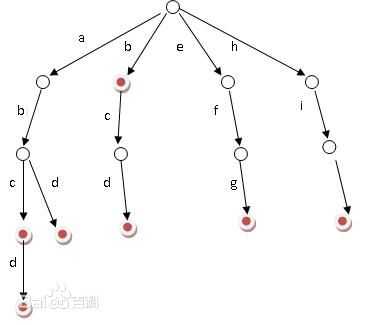
顾名思义,应该像英文字典一样查找。
先将root设为0。
每当插入一个单词时,从前向后遍历。
void insert(char* str) { int x=0,len=strlen(str); for(int i=0;i<=len-1;i++) { int id=str[i]-‘a‘+1; if(tree[x][id]==0) tree[x][id]=++tot; x=tree[x][id]; } return; }
举个栗子,已经插入了单词"internet","int","inside"。
在其中插入单词"interger"过程:
在根结点时,已经有i了,进入
在i结点时,已经有n了,进入
………………
在r结点时,此时r结点没有g儿子,所以新建结点,存储g
向下继续新建即可。
三、应用
有关前缀的问题很多都可以的啦
比如POJ2001 求唯一辨识前缀
给定n个单词,求对每个单词来说,取它多长的前缀可以在n个单词中唯一辨识此单词。
我们就可以构建字典树,搜索出最后一次分叉。
求最后一次分叉只需要在建树时将路径上所有节点的标记++,搜索时遇到标记为1返回,就是唯一辨识前缀了
void insert(char* str) { int x=0,len=strlen(str); for(int i=0;i<=len-1;i++) { int id=str[i]-‘a‘+1; if(tree[x][id]==0) tree[x][id]=++tot; x=tree[x][id]; vist[x]++; } return; }
int getans(char* str) { int x=0,len=strlen(str),i; for(i=0;i<len;i++) { int id=str[i]-‘a‘+1; x=tree[x][id]; cnt[i+1]=id; if(vist[x]==1) break; } return i+1; }
再比如hdu1251 求n个单词中以某单词为前缀的单词数量
在插入时 将路径上所有点打上标记
查询时直接输出末尾节点标记即可
int getans(char* str) { int x=0; for(int i=0;i<n;i++) { int id=str[i]-‘a‘+1; if(tree[x][id]==0) return 0; x=tree[x][id]; } return ans[x]; }
稍微难想一些的是HDU4285
先给一个数集
对于每个询问给出的数字x,求已知数集中与x异或最大的数
这个可以将数集中的每个数转换为二进制,以高位--->低位的顺序为字符串插入字典树
询问时搜索,
如果x的二进制第i位为0 且 根节点有id为1的儿子,就走1那一边
如果x的二进制第i位为1 且 根节点有id为0的儿子,就走0那一边
如果没有相反方向的儿子,就走自己的那边。
void insert(int xx,int num) { int x=0; for(int i=31;i>=0;i--) { int id=(xx&(1<<i))==0?0:1; if(tree[x][id]==0) tree[x][id]=++tot; x=tree[x][id]; } ed[x]=num; return; }
int getans(int xx) { int x=0; for(int i=31;i>=0;i--) { int id=(xx&(1<<i))==0?0:1; if(tree[x][id^1]==0) x=tree[x][id]; else x=tree[x][id^1]; } return a[ed[x]]; }
四、总结
字典树比较容易理解,代码简单。
所以在字符集大小*字符串总长度较小时,用字典树是要比hash优秀的,还不容易写错。
更新日期---2019.1.1 22:46
字典树(trie树)学习总结(例题讲解:POJ2001,HDU1251,HDU4825)
标签:大小 排序 进制 更新 长度 结构 不容易 code 问题
原文地址:https://www.cnblogs.com/666-233/p/10206453.html