标签:状态 string 输入输出格式 相同 相互 sample 初始 struct bec
原《奇怪的字符串》请前往 P2543
跳跳棋是在一条数轴上进行的。棋子只能摆在整点上。每个点不能摆超过一个棋子。
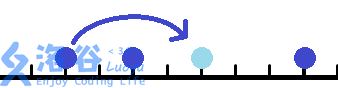
我们用跳跳棋来做一个简单的游戏:棋盘上有3颗棋子,分别在a,b,c这三个位置。我们要通过最少的跳动把他们的位置移动成x,y,z。(棋子是没有区别的)
跳动的规则很简单,任意选一颗棋子,对一颗中轴棋子跳动。跳动后两颗棋子距离不变。一次只允许跳过1颗棋子。
写一个程序,首先判断是否可以完成任务。如果可以,输出最少需要的跳动次数。
第一行包含三个整数,表示当前棋子的位置a b c。(互不相同)
第二行包含三个整数,表示目标位置x y z。(互不相同)
输出格式:
如果无解,输出一行NO。
如果可以到达,第一行输出YES,第二行输出最少步数。
20% 输入整数的绝对值均不超过10
40% 输入整数的绝对值均不超过10000
100% 绝对值不超过10^9
一道神仙题
我们发现一种状态的转移只有三种:
1.中间的往left跳
2.中间的往right跳
3.距离中间近的往里跳
然后我们发现前两种状态都有一种转移方法可以转移回来,这种状态就是第3种状态
于是我们可以将此时的状态为父亲结点,不转移第3种情况,形成一颗二叉树,一个是不会出现重复的状态,另一个是父亲和儿子可以相互转移,儿子的父亲就是儿子进行第3种转移,非常的好
当无法进行第3种转移时,即b-a==c-b,这时就是一棵树里的根,很显然,根不同的两棵树没有任何路径,即无法相互转移
这样问题就变成了找初始状态和终止状态的根,若相同就输出YES,反之就输出NO
这样的时间复杂度依旧是O(N),甚至会更恐怖
观察转移方法:找一个父亲以后是abs(a-b),min(a,b);
我们完全可以一次找到第一个比min(a-b)小的差,即max(a,b)%min(a,b),这样的时间复杂度就变成了和求gcd相同的时间复杂度,即O(logn)
求转移次数,我们可以想到用和LCA极其类似的方法:先将初始状态和终止状态的状态的深度变的相同,再不断向上跳,直到相同即可
细节很多,不一一列举了
上代码(代码丑的一批,除我以外能看明白的都不是一般dalao):
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define rep(i,a,b) for(long long i=a;i<=b;i++)
#define dwn(i,a,b) for(long long i=a;i>=b;i--)
using namespace std;
typedef long long ll;
struct zlk{
ll a,b,c,d;
}o,p,wyx,h,l1,l2;
bool check(){
if(o.a==p.a && p.b==o.b && p.c==o.c) return 1;
return 0;
}
bool check1(){
if(h.a==wyx.a && h.b==wyx.b && h.c==wyx.c) return 1;
return 0;
}
zlk gcd(ll c,zlk t){
if(t.b-t.a==t.c-t.b){
zlk res;
res.a=t.a; res.b=t.b;
res.c=t.c; res.d=c;
return res;
}
if(t.b-t.a>t.c-t.b){
int cha=(t.c-t.b);
t.b=t.a+(t.b-t.a)%(t.c-t.b);
if(t.a==t.b) t.b+=cha;
t.c=t.b+cha;
return gcd(c+1,t);
}
int cha=(t.b-t.a);
t.b=t.c-(t.c-t.b)%(t.b-t.a);
if(t.b==t.c) t.b-=cha;
t.a=t.b-cha;
return gcd(c+1,t);
}
ll lst,sum;
void work(zlk &t){
if(t.b-t.a>t.c-t.b){
int cha=(t.c-t.b);
sum+=(t.b-t.a)/(t.c-t.b);
lst+=(t.b-t.a)/(t.c-t.b);
t.b=t.a+(t.b-t.a)%(t.c-t.b);
if(t.a==t.b){
t.b+=cha,--sum;
--lst;
}
t.c=t.b+cha;
return;
}
int cha=(t.b-t.a);
sum+=(t.c-t.b)/(t.b-t.a);
lst+=(t.c-t.b)/(t.b-t.a);
t.b=t.c-(t.c-t.b)%(t.b-t.a);
if(t.b==t.c){
t.b-=cha,sum--;
--lst;
}
t.a=t.b-cha;
}
int main(){
scanf("%lld%lld%lld%lld%lld%lld",&wyx.a,&wyx.b,&wyx.c,&h.a,&h.b,&h.c);
if(wyx.a>wyx.c) swap(wyx.a,wyx.c);
if(wyx.a>wyx.b) swap(wyx.a,wyx.b);
if(wyx.b>wyx.c) swap(wyx.b,wyx.c);
o=gcd(0,wyx);wyx.d=o.d;
if(h.a>h.c) swap(h.a,h.c);
if(h.a>h.b) swap(h.a,h.b);
if(h.b>h.c) swap(h.b,h.c);
p=gcd(0,h);h.d=p.d;
if(!check()){printf("NO"); return 0;}
printf("YES\n");
if(h.d<wyx.d) swap(h.a,wyx.a),swap(h.b,wyx.b),swap(h.c,wyx.c),swap(h.d,wyx.d);
while(h.d>wyx.d){--h.d; work(h);}
if(check1()){
printf("%lld",sum);
return 0;
}
while(!check1()){
lst=0;
l1=h; l2=wyx;
work(h); work(wyx);
}
sum-=lst;
ll ans1=0,ans2=0;
if(l1.b-l1.a>l1.c-l1.b && l2.b-l2.a>l2.c-l2.b){
ans1=(l1.b-l1.a)/(l1.c-l1.b); ans2=(l2.b-l2.a)/(l2.c-l2.b);
sum+=abs(ans1-ans2);
}
else if(l1.b-l1.a<l1.c-l1.b && l2.b-l2.a<l2.c-l2.b){
ans1=(l1.c-l1.b)/(l1.b-l1.a); ans2=(l2.c-l2.b)/(l2.b-l2.a);
sum+=abs(ans1-ans2);
}
else{
if(l1.b-l2.a>l1.c-l1.b){
ans1=(l1.b-l1.a)/(l1.c-l1.b);
if((l1.b-l1.a)%(l1.c-l1.b)==0) --ans1;
}
else{
ans1=(l1.c-l1.b)/(l1.b-l1.a);
if((l1.c-l1.b)%(l1.b-l1.a)==0) --ans1;
}
if(l2.b-l2.a>l2.c-l2.b){
ans2=(l2.b-l2.a)/(l2.c-l2.b);
if((l2.b-l2.a)%(l2.c-l2.b)==0) --ans2;
}
else{
ans2=(l2.c-l2.b)/(l2.b-l2.a);
if((l2.c-l2.b)%(l2.b-l2.a)==0) --ans2;
}
sum+=ans1+ans2;
}
printf("%lld",sum);
return 0;
}
标签:状态 string 输入输出格式 相同 相互 sample 初始 struct bec
原文地址:https://www.cnblogs.com/handsome-zlk/p/10210913.html