标签:固定 之间 bre prim point 个数 std har nbsp
A:对每种商品多源bfs一下每个点到该商品的最近距离,对每个点sort一下取前s个即可。

#include<iostream> #include<cstdio> #include<cmath> #include<cstdlib> #include<cstring> #include<algorithm> using namespace std; #define ll long long #define int long long #define N 100010 int n,m,k,s,a[N],p[N],d[110][N],b[110],q[N],t; int read() { int x=0,f=1;char c=getchar(); while (c<‘0‘||c>‘9‘) {if (c==‘-‘) f=-1;c=getchar();} while (c>=‘0‘&&c<=‘9‘) x=(x<<1)+(x<<3)+(c^48),c=getchar(); return x*f; } struct data{int to,nxt; }edge[N<<1]; void addedge(int x,int y){t++;edge[t].to=y,edge[t].nxt=p[x],p[x]=t;} void bfs(int k) { int head=0,tail=0;memset(d[k],42,sizeof(d[k])); for (int i=1;i<=n;i++) if (a[i]==k) q[++tail]=i,d[k][i]=0; do { int x=q[++head]; for (int i=p[x];i;i=edge[i].nxt) if (d[k][edge[i].to]>d[k][x]) { d[k][edge[i].to]=d[k][x]+1; q[++tail]=edge[i].to; } }while (head<tail); } signed main() { #ifndef ONLINE_JUDGE freopen("a.in","r",stdin); freopen("a.out","w",stdout); #endif n=read(),m=read(),k=read(),s=read(); for (int i=1;i<=n;i++) a[i]=read(); for (int i=1;i<=m;i++) { int x=read(),y=read(); addedge(x,y),addedge(y,x); } for (int i=1;i<=k;i++) bfs(i); for (int i=1;i<=n;i++) { for (int j=1;j<=k;j++) b[j]=d[j][i]; sort(b+1,b+k+1); int ans=0; for (int j=1;j<=s;j++) ans+=b[j]; printf("%d ",ans); } return 0; }
B:看起来非常玄乎事实上只是说两人交换次数的奇偶性不同。考虑将原排列变成该排列的最小交换次数,也即n-置换的循环节,这个东西的奇偶性是与交换次数的奇偶性有关的,因为每次交换会合并或拆开置换的两个循环。或者可以发现逆序对的奇偶性也是与其相关的,因为显然交换只会对两位置之间的区间产生影响,如果之间的数比两位置上的数都小或都大显然没有影响,否则每有一个这样的数逆序对变化两个。同时两位置本身带来一个逆序对变化,这样总逆序对变化量肯定是奇数。

#include<iostream> #include<cstdio> #include<cmath> #include<cstdlib> #include<cstring> #include<algorithm> using namespace std; #define ll long long #define N 1000010 int read() { int x=0,f=1;char c=getchar(); while (c<‘0‘||c>‘9‘) {if (c==‘-‘) f=-1;c=getchar();} while (c>=‘0‘&&c<=‘9‘) x=(x<<1)+(x<<3)+(c^48),c=getchar(); return x*f; } int n,a[N]; bool flag[N]; ll s; signed main() { #ifndef ONLINE_JUDGE freopen("b.in","r",stdin); freopen("b.out","w",stdout); #endif n=read(); for (int i=1;i<=n;i++) a[i]=read(); int c=n; for (int i=1;i<=n;i++) if (!flag[i]) { c--;flag[i]=1; int x=a[i];while (!flag[x]) flag[x]=1,x=a[x]; } if ((c&1)) { if (n&1) cout<<"Petr";else cout<<"Um_nik"; } else { if (n&1) cout<<"Um_nik";else cout<<"Petr"; } return 0; }
1.5h之后C还是没有思路,自闭到结束。
result:rank 154
C:刚的过程中最接近正解的想法是对0~2n-1建一些辅助点,对每个点将每一位挖掉与其连边,然后将辅助节点取反后连边,但这样显然不对。事实上稍加(?)修改就行了。

#include<iostream> #include<cstdio> #include<cmath> #include<cstdlib> #include<cstring> #include<algorithm> using namespace std; #define ll long long #define N (1<<22) int read() { int x=0,f=1;char c=getchar(); while (c<‘0‘||c>‘9‘) {if (c==‘-‘) f=-1;c=getchar();} while (c>=‘0‘&&c<=‘9‘) x=(x<<1)+(x<<3)+(c^48),c=getchar(); return x*f; } int n,m,a[N],b[N],ans; bool flag[N<<1]; void dfs(int k) { flag[k]=1; if (k>(1<<m)) { if (!flag[a[k^(1<<m)]]) dfs(a[k^(1<<m)]); } else { for (int i=0;i<m;i++) if (!(k&(1<<i))&&!flag[k|(1<<i)]) dfs(k|(1<<i)); if (b[k^(1<<m)-1]&&!flag[b[k^(1<<m)-1]+(1<<m)]) dfs(b[k^(1<<m)-1]+(1<<m)); } } signed main() { #ifndef ONLINE_JUDGE freopen("c.in","r",stdin); freopen("c.out","w",stdout); #endif m=read(),n=read(); for (int i=1;i<=n;i++) b[a[i]=read()]=i; for (int i=(1<<m)+1;i<=(1<<m)+n;i++) if (!flag[i]) dfs(i),ans++; cout<<ans; return 0; }
D:题意莫名其妙,实际上是设f(x)为x所有分解因子方式中最小的因子和,求f(x) (x>=n)的最小值。一个古老的结论是因子之和固定时尽量取3能使乘积最大,有剩余时补2,于是只需考虑这样的数。求对数可以大致求出答案范围。枚举每一种可能,高精度求出即可。这需要多项式快速幂。于是就被各种问题折腾了一天。有多惨我已经不想回顾了,最后也不知道怎么过的。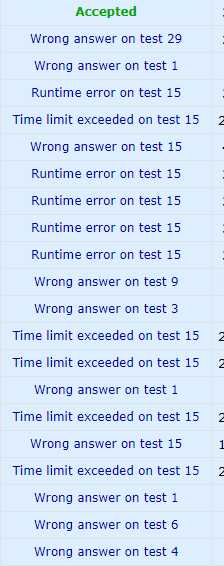

#include<iostream> #include<cstdio> #include<cmath> #include<cstdlib> #include<cstring> #include<algorithm> using namespace std; #define ll long long #define N (1<<19) #define M 1500010 int read() { int x=0,f=1;char c=getchar(); while (c<‘0‘||c>‘9‘) {if (c==‘-‘) f=-1;c=getchar();} while (c>=‘0‘&&c<=‘9‘) x=(x<<1)+(x<<3)+(c^48),c=getchar(); return x*f; } int n,a[M],r[N],len,ans=100000000; ll f[N],c[N]; char s[M]; const double PI=3.14159265358979323846; struct complex { double x,y; complex operator +(const complex&a) const { return (complex){x+a.x,y+a.y}; } complex operator -(const complex&a) const { return (complex){x-a.x,y-a.y}; } complex operator *(const complex&a) const { return (complex){x*a.x-y*a.y,x*a.y+y*a.x}; } }g[N],b[N]; void DFT(complex *a,int n,int op) { for (int i=0;i<n;i++) if (i<r[i]) swap(a[i],a[r[i]]); for (int i=2;i<=n;i<<=1) { complex wn=(complex){cos(2*PI/i),op*sin(2*PI/i)}; for (int j=0;j<n;j+=i) { complex w=(complex){1,0}; for (int k=j;k<j+(i>>1);k++,w=w*wn) { complex x=a[k],y=w*a[k+(i>>1)]; a[k]=x+y,a[k+(i>>1)]=x-y; } } } } int work(int n,int c) { c*=pow(3,n%6);n/=6; memset(f,0,sizeof(f));memset(b,0,sizeof(b));memset(g,0,sizeof(g)); g[0].x=1;b[0].x=729;int t; for (t=2;t<=(n<<1);t<<=1) { for (int i=0;i<t;i++) r[i]=(r[i>>1]>>1)|(i&1)*(t>>1); DFT(b,t,1); if (n&(t>>1)) { DFT(g,t,1); for (int i=0;i<t;i++) g[i]=g[i]*b[i]; DFT(g,t,-1); for (int i=0;i<t;i++) f[i]=g[i].x/t+0.5; for (int i=0;i<t;i++) if (f[i]>999) f[i+1]+=f[i]/1000,f[i]%=1000; for (int i=0;i<t;i++) g[i].x=f[i],g[i].y=0; } if (t>n) break; for (int i=0;i<t;i++) b[i]=b[i]*b[i]; DFT(b,t,-1); for (int i=0;i<t;i++) f[i]=b[i].x/t+0.5; for (int i=0;i<t;i++) if (f[i]>999) f[i+1]+=f[i]/1000,f[i]%=1000; for (int i=0;i<t;i++) b[i].x=f[i],b[i].y=0; } for (int i=0;i<t;i++) f[i]=g[i].x; for (int i=0;i<t;i++) f[i]=f[i]*c; for (int i=0;i<t;i++) if (f[i]>999) f[i+1]+=f[i]/1000,f[i]%=1000; while (f[t]==0) t--;return t+1; //c*729^n } int mul(ll *f,int c) { int n=N-1;while (f[n]==0) n--; for (int i=0;i<=n;i++) f[i]*=c; for (int i=0;i<=n;i++) f[i+1]+=f[i]/1000,f[i]%=1000; if (f[n+1]) n++; return n+1; } bool check(ll *f,int len) { int m=(n-1)/3+1; if (len>m) return 1; if (len<m) return 0; for (int i=m-1;~i;i--) if (f[i]!=a[i]) return f[i]>a[i]; return 1; } signed main() { #ifndef ONLINE_JUDGE freopen("d.in","r",stdin); freopen("d.out","w",stdout); #endif scanf("%s",s+1);n=strlen(s+1); for (int i=0;i<n;i++) a[i]=s[n-i]-‘0‘; if (n==1&&a[0]==1) {cout<<1;return 0;} for (int i=0;i<(n-1)/3+1;i++) a[i]=a[i*3]+a[i*3+1]*10+a[i*3+2]*100; len=work(max(floor((n-1)/log10(3))-1,0.0),1); for (int k=max(floor((n-1)/log10(3))-1,0.0);k<=ceil(n/log10(3))+1;k++) { memcpy(c,f,sizeof(c)); if (check(c,len)) {ans=min(ans,k*3);break;} if (check(c,mul(c,2))) {ans=min(ans,k*3+2);break;} if (check(c,mul(c,2))) {ans=min(ans,k*3+4);} len=mul(f,3); } cout<<ans; return 0; }
E:先考虑序列上怎么做。考虑每种质因子,问题变为求区间每个数和x取min之和。显然每个数的质因子数量不会很多,所以对每种质因子个数分别建个BIT即可,复杂度即为log2。可以线性筛预处理做到log分解质因数。树上问题直接树剖的话是log3,不太能接受,可以通过欧拉序去一个log,即在进入子树时加,退出子树时减。我又被,卡常了。

#include<iostream> #include<cstdio> #include<cmath> #include<cstdlib> #include<cstring> #include<algorithm> #include<vector> using namespace std; #define ll long long #define N 100010 #define M 10000000 #define P 1000000007 int read() { int x=0,f=1;char c=getchar(); while (c<‘0‘||c>‘9‘) {if (c==‘-‘) f=-1;c=getchar();} while (c>=‘0‘&&c<=‘9‘) x=(x<<1)+(x<<3)+(c^48),c=getchar(); return x*f; } int n,p[N],a[N],prime[M+10],minp[M+10],deep[N],fa[N][20],in[N],out[N],ans[N],tree[30][N<<1],cnt,m,t; bool flag[M+10],tmp[30]; struct data{int to,nxt; }edge[N<<1]; struct data2{int x,y,z,lca; }q[N]; struct data3{int x,cnt;}; vector<data3> point[M+10],Q[M+10]; void addedge(int x,int y){t++;edge[t].to=y,edge[t].nxt=p[x],p[x]=t;} void add(int p,int k,int x){while (k<=2*n) tree[p][k]+=x,k+=k&-k;} int query(int p,int k){int s=0;while (k) s+=tree[p][k],k-=k&-k;return s;} int ksm(int a,int k) { int s=1; for (;k;k>>=1,a=1ll*a*a%P) if (k&1) s=1ll*s*a%P; return s; } void dfs(int k) { in[k]=out[k]=++cnt; for (int i=p[k];i;i=edge[i].nxt) if (edge[i].to!=fa[k][0]) { fa[edge[i].to][0]=k; deep[edge[i].to]=deep[k]+1; dfs(edge[i].to); out[k]=++cnt; } } int lca(int x,int y) { if (deep[x]<deep[y]) swap(x,y); for (int j=19;~j;j--) if (deep[fa[x][j]]>=deep[y]) x=fa[x][j]; if (x==y) return x; for (int j=19;~j;j--) if (fa[x][j]!=fa[y][j]) x=fa[x][j],y=fa[y][j]; return fa[x][0]; } int main() { #ifndef ONLINE_JUDGE freopen("e.in","r",stdin); freopen("e.out","w",stdout); #endif flag[1]=1;cnt=0; for (int i=2;i<=M;i++) { if (!flag[i]) prime[++cnt]=i,minp[i]=i; for (int j=1;j<=cnt&&prime[j]*i<=M;j++) { flag[prime[j]*i]=1; minp[prime[j]*i]=prime[j]; if (i%prime[j]==0) break; } } n=read(); for (int i=1;i<n;i++) { int x=read(),y=read(); addedge(x,y),addedge(y,x); } cnt=0;dfs(1); fa[1][0]=1; for (int j=1;j<20;j++) for (int i=1;i<=n;i++) fa[i][j]=fa[fa[i][j-1]][j-1]; for (int i=1;i<=n;i++) { int x=a[i]=read(); while (x>1) { int y=minp[x],cnt=0; while (minp[x]==y) cnt++,x/=y; point[y].push_back((data3){i,cnt}); } } m=read();cnt=0; for (int i=1;i<=m;i++) { q[i].x=read(),q[i].y=read(),q[i].z=read();q[i].lca=lca(q[i].x,q[i].y);ans[i]=1; int x=q[i].z; while (x>1) { int y=minp[x],cnt=0; while (minp[x]==y) cnt++,x/=y; Q[y].push_back((data3){i,cnt}); } } fa[1][0]=0; int u=25; for (int i=1;i<=M;i++) if (!flag[i]) { while (ksm(i,u)>M) u--; for (int j=0;j<point[i].size();j++) { add(point[i][j].cnt,in[point[i][j].x],1); add(point[i][j].cnt,out[point[i][j].x]+1,-1); tmp[point[i][j].cnt]=1; } for (int j=0;j<Q[i].size();j++) { ll x=0; for (int k=1;k<=Q[i][j].cnt;k++) if (tmp[k]) x+=k*(query(k,in[q[Q[i][j].x].x])+query(k,in[q[Q[i][j].x].y])+ 1ll*(P-2)*query(k,in[q[Q[i][j].x].lca])%(P-1)+1ll*(P-2)*query(k,in[fa[q[Q[i][j].x].lca][0]])%(P-1)); for (int k=Q[i][j].cnt+1;k<=u;k++) if (tmp[k]) x+=Q[i][j].cnt*(query(k,in[q[Q[i][j].x].x])+query(k,in[q[Q[i][j].x].y])+ 1ll*(P-2)*query(k,in[q[Q[i][j].x].lca])%(P-1)+1ll*(P-2)*query(k,in[fa[q[Q[i][j].x].lca][0]])%(P-1)); ans[Q[i][j].x]=1ll*ans[Q[i][j].x]*ksm(i,((x%(P-1))+P-1)%(P-1))%P; } for (int j=0;j<point[i].size();j++) { add(point[i][j].cnt,in[point[i][j].x],-1); add(point[i][j].cnt,out[point[i][j].x]+1,1); tmp[point[i][j].cnt]=0; } } for (int i=1;i<=m;i++) printf("%d\n",ans[i]); return 0; }
Codeforces Round #485 Div. 1 vp记
标签:固定 之间 bre prim point 个数 std har nbsp
原文地址:https://www.cnblogs.com/Gloid/p/10211755.html