标签：shu   方法   query   name   还需要   define   tis   cstring   --   

Tourists

UOJ 30

题目大意

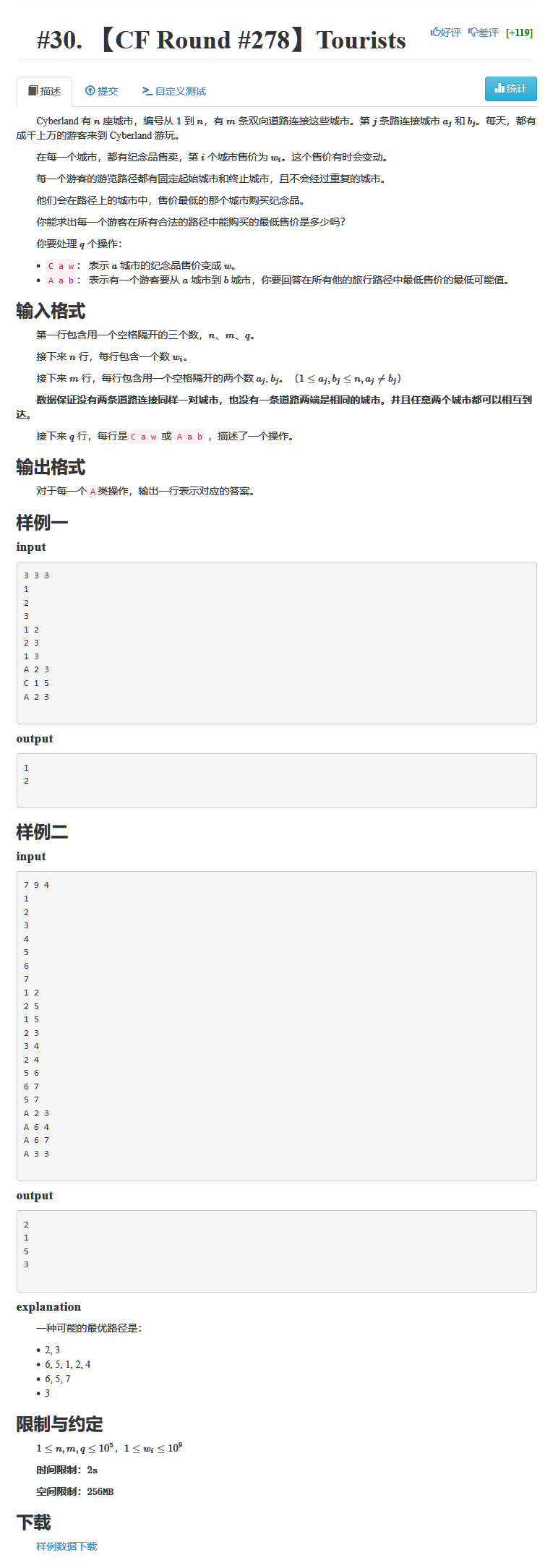
\(n\) 个 \(m\) 条边的无向图，每个点有点权 \(w_i\) ， \(q\) 次询问，每次修改第 \(a\) 个点的点权为 \(w\) ，或者查询 \(a\) 到 \(b\) 所有路径中，最小的点权

数据范围

\(1 \le n,m,q \le 10^5, 1 \le w_i \le 10^9\)

时空限制

2s，256MB

分析

对于这种在无向图上查询路径信息的题，一般利用圆方树将其转为树上问题

对于一个方点，维护点双中最小的点权，但是如果这样，每修改一次就需要修改所有与它相邻的节点。

对此我们有一个经典方法，对于方点维护除了环顶之外的信息，在圆方树中就相当于方点维护所有它儿子的信息，那么我们修改时只需要修改它的父亲，查询的时候如果 \(lca\) 为方点，那么还需要加上它的父亲的信息（因为父亲也在此点双中）

Code

#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
#include <set>

using namespace std;

template<class T> void read(T & x)
{
    x = 0; int f = 1, ch = getchar();
    while(ch < ‘0‘ || ch > ‘9‘)
    {
        if(ch == ‘-‘) f = -1;
        ch = getchar();
    }
    while(ch >= ‘0‘ && ch <= ‘9‘)
    {
        x = x * 10 - ‘0‘ + ch;
        ch = getchar();
    }
    x *= f;
}

#define lson u << 1, l, mid
#define rson u << 1 | 1, mid + 1, r

const int inf = 1000000000;

const int maxn = 100000 + 5;
const int maxm = 100000 + 5;
const int maxe = maxm * 2;
const int maxnode = maxn * 2;

int n, m, q;
int val[maxnode];

struct edge
{
    int to, nex;
    edge(int to = 0, int nex = 0) : to(to), nex(nex) {}
} g[maxe];
int head[maxn];
int ecnt;
vector<int> adj[maxnode];

inline void addedge(int u, int v)
{
    g[ecnt] = edge(v, head[u]), head[u] = ecnt++;
    g[ecnt] = edge(u, head[v]), head[v] = ecnt++;
}
inline void adde(int u, int v)
{
    adj[u].push_back(v);
    adj[v].push_back(u);
}

int dfc, dfn[maxn], low[maxn];
int top, sta[maxn];
int bcnt;
multiset<int> bccval[maxn];

void tarjan(int u, int fa)
{
    dfn[u] = low[u] = ++dfc;
    sta[++top] = u;
    for(int i = head[u]; ~ i; i = g[i].nex)
    {
        int v = g[i].to;
        if(v != fa)
        {
            if(!dfn[v])
            {
                tarjan(v, u);
                low[u] = min(low[u], low[v]);
                if(low[v] >= dfn[u])
                {
                    int now = n + (++bcnt);
                    adde(now, u);
                    while(true)
                    {
                        int x = sta[top--];
                        bccval[bcnt].insert(val[x]);
                        adde(now, x);
                        if(x == v) break;
                    }
                    val[now] = * bccval[bcnt].begin();
                }
            }
            else low[u] = min(low[u], dfn[v]);
        }
    }
}

struct segment_tree
{
    int mn[maxnode << 2];

    inline void pushup(int u)
    {
        mn[u] = min(mn[u << 1], mn[u << 1 | 1]);
    }
    void build(int u, int l, int r)
    {
        if(l == r)
        {
            mn[u] = val[ver[l]];
            return;
        }
        int mid = (l + r) >> 1;
        build(lson), build(rson);
        pushup(u);
    }
    void update(int u, int l, int r, int qp)
    {
        if(l == r)
        {
            mn[u] = val[ver[l]];
            return;
        }
        int mid = (l + r) >> 1;
        if(qp <= mid) update(lson, qp);
        else update(rson, qp);
        pushup(u);
    }
    int query(int u, int l, int r, int ql, int qr)
    {
        if(l == ql && r == qr) return mn[u];
        int mid = (l + r) >> 1;
        if(qr <= mid) return query(lson, ql, qr);
        else if(ql > mid) return query(rson, ql, qr);
        else
        {
            int lv = query(lson, ql, mid);
            int rv = query(rson, mid + 1, qr);
            return min(lv, rv);
        }
    }

    int dep[maxnode], anc[maxnode], siz[maxnode], son[maxnode];
    int dfn[maxnode], top[maxnode], ver[maxnode], dfc;

    void dfs1(int u)
    {
        siz[u] = 1;
        for(unsigned int i = 0; i < adj[u].size(); ++i)
        {
            int v = adj[u][i];
            if(v != anc[u])
            {
                dep[v] = dep[u] + 1;
                anc[v] = u;
                dfs1(v);
                siz[u] += siz[v];
                if(siz[son[u]] <= siz[v]) son[u] = v;
            }
        }
    }
    void dfs2(int u, int chain)
    {
        top[u] = chain;
        dfn[u] = ++dfc;
        ver[dfc] = u;
        if(son[u])
        {
            dfs2(son[u], chain);
        }
        for(unsigned int i = 0; i < adj[u].size(); ++i)
        {
            int v = adj[u][i];
            if(v != anc[u] && v != son[u])
            {
                dfs2(v, v);
            }
        }
    }
    void init()
    {
        dfs1(1);
        dfs2(1, 1);
        build(1, 1, n + bcnt);
    }

    void update(int u, int x)
    {
        int v = anc[u];
        if(v) bccval[v - n].erase(bccval[v - n].find(val[u]));
        val[u] = x;
        if(v) bccval[v - n].insert(val[u]);
        if(v) val[v] = * bccval[v - n].begin();
        update(1, 1, n + bcnt, dfn[u]);
        if(v) update(1, 1, n + bcnt, dfn[v]);
    }
    int query(int u, int v)
    {
        int re = inf;
        while(top[u] != top[v])
        {
            if(dep[top[u]] > dep[top[v]]) swap(u, v);
            re = min(re, query(1, 1, n + bcnt, dfn[top[v]], dfn[v]));
            v = anc[top[v]];
        }
        if(dep[u] > dep[v]) swap(u, v);
        re = min(re, query(1, 1, n + bcnt, dfn[u], dfn[v]));
        if(u > n)
        {
            re = min(re, val[anc[u]]);
        }
        return re;
    }
} seg;

void init()
{
    tarjan(1, 0);
    seg.init();
}

int main()
{
    // freopen("testdata.in", "r", stdin);
    read(n), read(m), read(q);
    for(int i = 1; i <= n; ++i)
    {
        read(val[i]);
    }
    memset(head, -1, sizeof(head));
    for(int i = 1; i <= m; ++i)
    {
        int u, v; read(u), read(v);
        addedge(u, v);
    }
    init();
    for(int i = 1; i <= q; ++i)
    {
        char op[5]; scanf("%s", op);
        if(op[0] == ‘C‘)
        {
            int a, w; read(a), read(w);
            seg.update(a, w);
        }
        else
        {
            int a, b; read(a), read(b);
            printf("%d\n", seg.query(a, b));
        }
    }
    return 0;
}

UOJ 30 【CF Round #278】Tourists

标签：shu   方法   query   name   还需要   define   tis   cstring   --   

原文地址：https://www.cnblogs.com/ljzalc1022/p/10218456.html