标签:inf using 产生 col src while main 图片 bool
题目描述
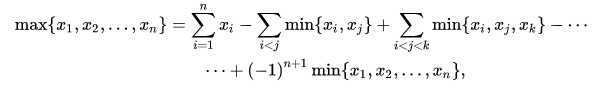
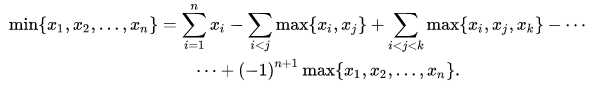
大概就是这么两个东西,做题思路大概就是正难则反吧,max不好求但min好求,就可以直接用这种方法上了。
现在我们算maxV(S),然鹅它不好算,所以我们就转换求所有minV(S)。
考虑一个事件发生的概率为p,那么我们就有了求min的方法。
sum=1*p+2*(p-1)*p+3*(p-1)^2*p......
然后用高中数学知识,解得它等于1/p。
然后我们的任务变成了求所有子集的p。
这玩意也不太好求,因为所有与这个集合有交的数都会产生贡献。
再次正难则反一下,变成了1-补集,这个补集和很好,它就是补集的高维前缀和。
有人说这是FMT,但好像FWT的异或卷积也长这样?
代码
#include<iostream> #include<cstdio> #include<cmath> #define N (1<<20)+20 using namespace std; const double eps=1e-10; int n,size,cnt[N]; double ans,a[N]; inline int rd(){ int x=0;char c=getchar();bool f=0; while(!isdigit(c)){if(f==‘-‘)f=1;c=getchar();} while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();} return f?-x:x; } int main(){ n=rd();size=(1<<n);int up=size; for(int i=0;i<size;++i)scanf("%lf",&a[i]); for(int i=1;i<size;i<<=1) for(int j=0;j<size;++j)if(!(j&i))a[j|i]+=a[j]; for(int i=1;i<=size;++i)cnt[i]=cnt[i>>1]+(i&1); for(int i=1;i<size;++i){ double x=1-a[(size-1)^i]; if(fabs(x)<eps){printf("INF\n");return 0;} if(cnt[i]&1)ans+=(double)1/x;else ans-=(double)1/x; } printf("%.10lf",ans); return 0; }
我看到网上还有这么一种解法
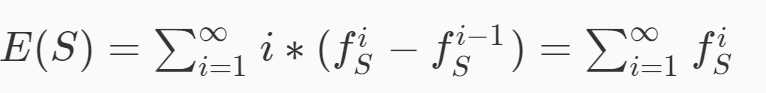
然而我并没有看懂。。。
标签:inf using 产生 col src while main 图片 bool
原文地址:https://www.cnblogs.com/ZH-comld/p/10222235.html