标签:正整数 简单 存储 bubuko 思路 包括 位置 结构 for语句
问题描述:给定一整数序列A1,A2,...,An(可含负数),求A1-An中的一个子序列Ai-Aj,使得Ai-Aj的和最大,求该和的值。
涉及变量:sequence:int[]型常量,给定整数序列
n:实际元素个数
sum:int型变量,子序列之和
max:int型变量,最大子序列之和
i:int型变量,下标
涉及教材:《数据结构——Java语言描述(第2版)》 清华大学出版社
第一次看到这道题时我的思路是用三个for循环解决问题:
1.将max的初值赋为sequence[0]
2.从下标为0,1,..,n-1的位置开始计算每一个子序列的和并存放在sum变量中
3.比较sum与max,若sum>max,则将max赋值为sum所存储值,否则不变
4.结束for循环后,返回max
这种简单粗暴的方法,原理简单,但没有太多技巧,说白了就是全部算一遍,费时费力。其时间复杂度为O(n^3),当序列较大时不适合使用这种方法
第二次看到这道题是在教科书上,书上介绍了4种关于该问题的求解方式,包括上面我第一次想到的思路且有其改良版,但此处只讲我最喜欢的一种算法的思路:
1.将max和sum都赋初值为0
2.当i<sequence.length,for循环中执行每一个数加到sum中
3.若sum>max,则将max赋值为sum
4.若sum<0,将sum清空为0重新开始计算
5.结束for循环后,返回max
第4步操作是因为若前面的子序列之和小于0,则必定会影响后面正整数子序列之和,使其无法达到最大子序列之和,故将其赋值为0,表示从这一元素开始重新计算子序列之和
书上代码如下:
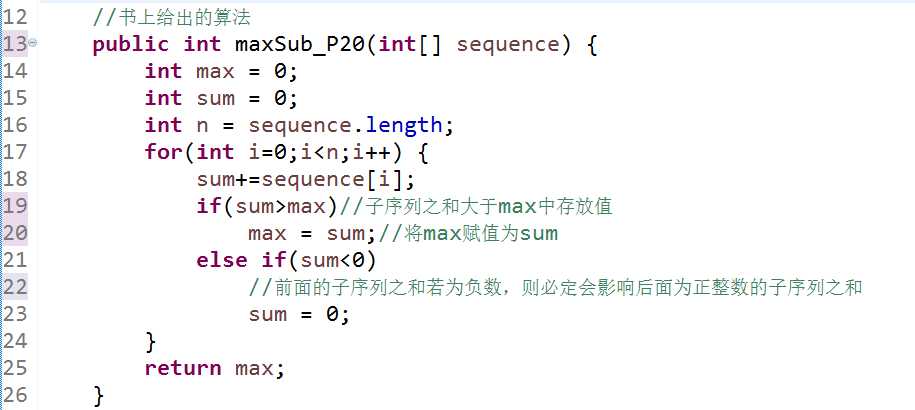
第4步十分巧妙地避免了重算子序列的麻烦,但同时由于这一步,这个算法对整个序列都为负数时无能为力
为了能解决全负数的序列求和问题,我改良了这个算法
我的思路:
1.将max赋值为sequence[0],sum赋值为0
2.用for语句开始执行子序列最大求和的运算和对比,循环结束条件为对数组各元素的一次遍历结束后
3.每次执行sum+=sequence[i],即求子序列之和
4.若sum>max时,有两种可能
(1)sequence[i]比sum大,sum由于前面存在的负数而影响了sum的最大可能,此时将max赋值为sum
(2)其他情况,sum>=sequence[i],将max赋值为sum
5.当sum小于0时,会对最大子序列之和造成影响,故将sum清零重新计算
//这一步可能有人会奇怪4和5似乎相互矛盾了,上一步当sum<0时不是已经被清零了吗,下一次怎么又会在第一个if里出现小于0的情况,这里是考虑到了全负数序列的情况
假设所给出序列为 {-6,-2,-1},
第1次循环时max=-6,sum=-6,不符合if执行条件,进入else if,sum=0,i=1
第2次循环时max=-6,sum=-2,符合sum>max的if执行条件,且执行else语句,得max=-2,sum=0,i=2
第3次循环时max=-2,sum=-1,符合sum>max的if执行条件,其符合里面的if(sequence[i]>sum)的执行条件,得max=-1,sum=0,i=3,结束循环
以下为代码:

代码本身的for循环其实可以用do_while循环替代,思路大体不变
以上是我关于子序列求和的部分思考和代码,希望对各位有所帮助
190111 Rewivy
标签:正整数 简单 存储 bubuko 思路 包括 位置 结构 for语句
原文地址:https://www.cnblogs.com/rewivy/p/10255723.html