标签:lex 1.4 计算器 let fill ali bool val 并且
菜菜呀,个税最近改革了,我得重新计算你的工资呀,我需要个计算器,你开发一个吧

X总,咱不会买一个吗?

那不得花钱吗,一块钱也是钱呀··这个计算器支持加减乘除运算就行,很简单

(尼玛)那能不能给我涨点工资呀?

公司现在很困难,你这个计算器关系到公司的存亡,你要注意呀!!

(关于撇开话题佩服的五体投地)好吧X总,我尽快做

给你一天时间,我这里着急要用

.........



有人说数据结构是为算法服务的,我还要在加一句:数据结构和算法都是为业务服务的!!
CXO的需求果然不同凡响,又让菜菜想到了新的数据结构:栈

定义
栈(stack)又名堆栈,它是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。
栈作为一种数据结构,其中有几个特性需要提起大家注意:
1. 操作受限:何为操作受限?在栈的操作中,一般语言中针对栈的操作只有两种:入栈和出栈。并且操作只发生在栈的顶部。 有的同学会问,我用其他数据结构也一样能实现栈的效果。不错,但是每种数据结构都有自己的使用场景,没有一种绝对无用的数据结构。
2. 栈在数据结构上属于一种线性表,满足后进先出的原则。这也是栈的最大特性,几乎大部分后进先出的场景都可以使用栈这个容器。比如一个函数的调用过程中,局部变量的存储就是栈原理。当执行一个函数结束的时候,局部变量其实最先释放的是最后的局部变量。
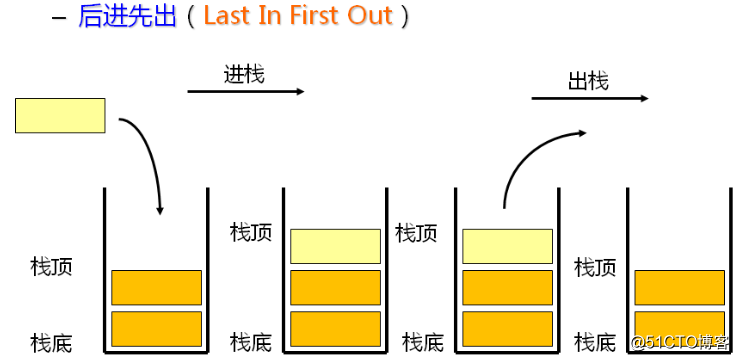
在内存分布上栈是用是实现的呢?既然栈是一种线性结构,也就说可以用线性的内存分布数据结构来实现。
1. 数组实现栈(顺序栈):数组是在内存分布上连续的一种数据结构。经过以前的学习,我们知道数组的容量是不变的。如果业务上可以知道一个栈的元素的最大数量,我们完全可以用数组来实现。为什么这么说?因为数组的扩容在某些时候性能是比较低的。因为需要开辟新空间,并发生复制过程。
class MyStack
{
//数组容器
int[] container = new int[100];
//栈顶元素的索引
int TopIndex = -1;
//入栈操作
public void Push(int newValue)
{
if (TopIndex >= 99)
{
return ;
}
TopIndex++;
container[TopIndex] = newValue;
}
//出栈操作
public int Pop()
{
if (TopIndex < 0)
{
return 0;
}
var topValue = container[TopIndex];
TopIndex--;
return topValue;
}
}
2. 链表实现栈(链式栈):为了应对数组的扩容问题,我们可以用链表来实现栈。栈的顶部元素永远指向链表的头元素即可。具体代码有兴趣的同学可以实现一下。
由以上可以看出,栈其实是基于基础数据结构之上的一个具体业务形式的封装即:先进后出。
基于数组的栈我们暂且只讨论未发生数组重建的场景下。无论是数组实现还是链表实现,我们发现栈的内部其实是有一个指向栈顶元素的指针,不会发生遍历数组或者链表的情形,所以栈的出栈操作时间复杂度为O(1)。
至于入栈,如果你看过我以前介绍数组和链表的文章,你可以知道,给一个数组下标元素赋值的操作时间复杂度为O(1),在链表头部添加一个元素的操作时间复杂度也是O(1)。所以无论是数组还是链表实现栈,入栈操作时间复杂度也是O(1)。并且栈只有入栈出栈两种操作,比其他数据结构有N个操作方法要简单很多,也不容易出错。
至于发生数组重建,copy全部数据的过程其实是一个顺序栈最坏的时间复杂度,因为和原数组的元素个数n有关,所以时间复杂度为O(n)
那一个计算器怎么用栈来实现呢?其实很多编译器就是通过两个栈来实现的,其中一个栈保存操作的数,另一个栈保存运算符。
我们从左到右遍历表达式,当遇到数字,我们直接压入操作数栈;当遇到操作符的时候,当前操作符与操作符栈顶的元素比较优先级(先乘除后加减的原则)。如果当前运算符比栈顶运算符优先级高,那说明不需要执行栈顶运算符运算,我们直接将当前运算符也入栈;
如果当前运算符比栈顶运算符优先级低,那说明该执行栈顶运算符的运算了。然后出栈运算符栈顶元素,数据栈顶两个元素,然后进行相关运算,然后把运算结果再次压入数据栈。
class Program
{
static void Main(string[] args)
{
List<string> lstAllData = new List<string>();
//读取输入的表达式,并整理
string inputStr = Console.ReadLine();
string tempData = "";
for (int i = 0; i < inputStr.Length; i++)
{
if (inputStr[i] == ‘+‘ || inputStr[i] == ‘-‘ || inputStr[i] == ‘*‘ || inputStr[i] == ‘/‘)
{
lstAllData.Add(tempData);
lstAllData.Add(inputStr[i].ToString());
tempData = "";
}
else
{
tempData += inputStr[i];
}
if(i== inputStr.Length - 1)
{
lstAllData.Add(tempData);
}
}
foreach (var item in lstAllData)
{
Calculator.Cal(item.ToString());
}
var ret = Calculator.GetResult();
Console.WriteLine(ret);
Console.Read();
}
}
//计算器
class Calculator
{
//存放计算数据的栈
static Stack<int> DataStack = new Stack<int>();
//存放操作符的栈
static Stack<string> OperatorStack = new Stack<string>();
public static int Cal(string dataOrOperator)
{
int data;
bool isData = int.TryParse(dataOrOperator, out data);
if (isData)
{
//如果是数据直接入数据栈
DataStack.Push(data);
}
else
{
//如果是操作符,和栈顶操作符比较优先级,如果大于栈顶,则直接入栈,否则栈顶元素出栈 进行操作
if (OperatorStack.Count <= 0)
{
OperatorStack.Push(dataOrOperator);
}
else
{
//当前运算符的优先级
var currentOpePrecedence = OperatorPrecedence(dataOrOperator);
//当前运算符栈顶元素的优先级
var stackTopOpePrecedence = OperatorPrecedence(OperatorStack.Peek());
if (currentOpePrecedence > stackTopOpePrecedence)
{
//如果当前运算符的优先级大于栈顶元素的优先级,则入栈
OperatorStack.Push(dataOrOperator);
}
else
{
//运算符栈顶元素出栈,数据栈出栈两个元素,然后进行运算
var stackOpe = OperatorStack.Pop();
var data2 = DataStack.Pop();
var data1 = DataStack.Pop();
var ret = CalculateData(stackOpe, data1, data2);
DataStack.Push(ret);
OperatorStack.Push(dataOrOperator);
}
}
}
return 0;
}
//获取表达式最后的计算结果
public static int GetResult()
{
var ret = 0;
while (OperatorStack.Count > 0)
{
var stackOpe = OperatorStack.Pop();
var data2 = DataStack.Pop();
var data1 = DataStack.Pop();
ret = CalculateData(stackOpe, data1, data2);
DataStack.Push(ret);
}
return ret;
}
//根据操作符进行运算,这里可以抽象出接口,请自行实现
static int CalculateData(string operatorString, int data1, int data2)
{
switch (operatorString)
{
case "+":
return data1 + data2;
case "-":
return data1 - data2;
case "*":
return data1 * data2;
case "/":
return data1 + data2;
default:
return 0;
}
}
//获取运算符优先级
public static int OperatorPrecedence(string a) //操作符优先级
{
int i = 0;
switch (a)
{
case "+": i = 1; break;
case "-": i = 1; break;
case "*": i = 2; break;
case "/": i = 2; break;
}
return i;
}
}
运行结果:
10+20*3+10-10+20-20+60*2
190
package stack
import (
"errors"
"fmt"
)
type Stack struct {
Element []interface{} //Element
}
func NewStack() *Stack {
return &Stack{}
}
func (stack *Stack) Push(value ...interface{}) {
stack.Element = append(stack.Element, value...)
}
//返回下一个元素
func (stack *Stack) Top() (value interface{}) {
if stack.Size() > 0 {
return stack.Element[stack.Size()-1]
}
return nil //read empty stack
}
//返回下一个元素,并从Stack移除元素
func (stack *Stack) Pop() (value interface{}) {
if stack.Size() > 0 {
d := stack.Element[stack.Size()-1]
stack.Element = stack.Element[:stack.Size()-1]
return d
}
return nil
}
//交换值
func (stack *Stack) Swap(other *Stack) {
switch {
case stack.Size() == 0 && other.Size() == 0:
return
case other.Size() == 0:
other.Element = stack.Element[:stack.Size()]
stack.Element = nil
case stack.Size() == 0:
stack.Element = other.Element
other.Element = nil
default:
stack.Element, other.Element = other.Element, stack.Element
}
return
}
//修改指定索引的元素
func (stack *Stack) Set(idx int, value interface{}) (err error) {
if idx >= 0 && stack.Size() > 0 && stack.Size() > idx {
stack.Element[idx] = value
return nil
}
return errors.New("Set失败!")
}
//返回指定索引的元素
func (stack *Stack) Get(idx int) (value interface{}) {
if idx >= 0 && stack.Size() > 0 && stack.Size() > idx {
return stack.Element[idx]
}
return nil //read empty stack
}
//Stack的size
func (stack *Stack) Size() int {
return len(stack.Element)
}
//是否为空
func (stack *Stack) Empty() bool {
if stack.Element == nil || stack.Size() == 0 {
return true
}
return false
}
//打印
func (stack *Stack) Print() {
for i := len(stack.Element) - 1; i >= 0; i-- {
fmt.Println(i, "=>", stack.Element[i])
}
}
package calculator
import (
"calculator/stack"
"strconv"
)
type Calculator struct{}
var DataStack *stack.Stack
var OperatorStack *stack.Stack
func NewCalculator() *Calculator {
DataStack = stack.NewStack()
OperatorStack = stack.NewStack()
return &Calculator{}
}
func (c *Calculator) Cal(dataOrOperator string) int {
if data, ok := strconv.ParseInt(dataOrOperator, 10, 64); ok == nil {
//如果是数据直接入数据栈
// fmt.Println(dataOrOperator)
DataStack.Push(data)
} else {
//如果是操作符,和栈顶操作符比较优先级,如果大于栈顶,则直接入栈,否则栈顶元素出栈 进行操作
if OperatorStack.Size() <= 0 {
OperatorStack.Push(dataOrOperator)
} else {
//当前运算符的优先级
currentOpePrecedence := operatorPrecedence(dataOrOperator)
//当前运算符栈顶元素的优先级
stackTopOpePrecedence := operatorPrecedence(OperatorStack.Top().(string))
if currentOpePrecedence > stackTopOpePrecedence {
//如果当前运算符的优先级大于栈顶元素的优先级,则入栈
OperatorStack.Push(dataOrOperator)
} else {
//运算符栈顶元素出栈,数据栈出栈两个元素,然后进行运算
stackOpe := OperatorStack.Pop()
data2 := DataStack.Pop()
data1 := DataStack.Pop()
ret := calculateData(stackOpe.(string), data1.(int64), data2.(int64))
DataStack.Push(ret)
OperatorStack.Push(dataOrOperator)
}
}
}
return 0
}
func (c *Calculator) GetResult() int64 {
var ret int64
for {
if OperatorStack.Size() > 0 {
stackOpe := OperatorStack.Pop()
data2 := DataStack.Pop()
data1 := DataStack.Pop()
ret = calculateData(stackOpe.(string), data1.(int64), data2.(int64))
DataStack.Push(ret)
} else {
break
}
}
return ret
}
func calculateData(operatorString string, data1, data2 int64) int64 {
switch operatorString {
case "+":
return data1 + data2
case "-":
return data1 - data2
case "*":
return data1 * data2
case "/":
return data1 + data2
default:
return 0
}
}
func operatorPrecedence(a string) int {
i := 0
switch a {
case "+":
i = 1
case "-":
i = 1
case "*":
i = 2
case "/":
i = 2
}
return i
}
package main
import (
"calculator/calculator"
"flag"
"fmt"
)
var (
inputStr = flag.String("input", "", "请输入...")
)
func main() {
flag.Parse()
var lstAllData []string
var tempData string
rs := []rune(*inputStr)
for i := 0; i < len(rs); i++ {
if string(rs[i]) == "+" || string(rs[i]) == "-" || string(rs[i]) == "*" || string(rs[i]) == "/" {
lstAllData = append(lstAllData, tempData)
lstAllData = append(lstAllData, string(rs[i]))
tempData = ""
} else {
tempData += string(rs[i])
}
if i == len(rs)-1 {
lstAllData = append(lstAllData, tempData)
}
}
ca := calculator.NewCalculator()
for _, v := range lstAllData {
ca.Cal(v)
}
ret := ca.GetResult()
fmt.Println(ret)
}
运算结果:
go run program.go -input=1+2-1*3
结果:0X总的个人空间需求并没有结束,菜菜仍然在持续优化中,欢迎大佬指正

标签:lex 1.4 计算器 let fill ali bool val 并且
原文地址:https://www.cnblogs.com/zhanlang/p/10259343.html