2019雅礼集训 D7T3 convex [咕咕咕]

标签：NPU   for   printf   alt   数据   getch   题解   sig   bubuko   

题目描述：

样例：

input1:
5
2 4
2 7
5 7
5 4
3 -2

output1:
90

input2:
4
-1000000000 1000000000
1000000000 1000000000
1000000000 -1000000000
-1000000000 -1000000000

output2:
0

数据范围与约定：

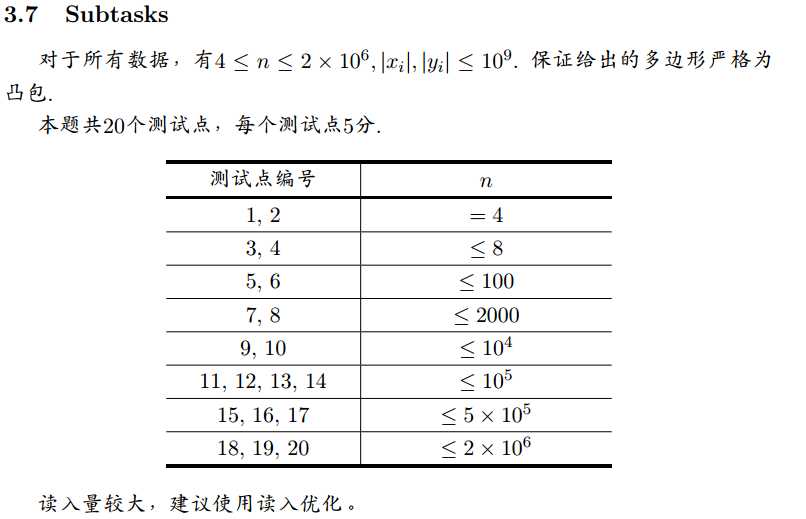
标签：计算几何

题解：

标程：

#include <bits/stdc++.h>

#define getchar getchar_unlocked
#define For(i, j, k) for (int i = j; i <= k; i++)

using namespace std;

const int Mod = 1e9 + 7;
const int N = 4e6 + 10;

int Read() {
    char c = getchar(); int x = 0, sig = 1;
    while (c > ‘9‘ || c < ‘0‘) sig = c == ‘-‘ ? -1 : sig, c = getchar();
    while (c >= ‘0‘ && c <= ‘9‘) x = x * 10 + c - ‘0‘, c = getchar();
    return x * sig;
}

typedef long long LL;

struct Point {
    int x, y;
};

typedef Point Vector;

Vector operator - (Vector u, Vector v) { return (Vector){u.x - v.x, u.y - v.y}; }
LL Cross(Vector u, Vector v) { return 1ll * u.x * v.y - 1ll * v.x * u.y; }

int n;
Point P[N];
int sumx[N], sumy[N];
LL sums[N];
int s1[N], s2[N];

int main() {

    freopen("convex.in", "r", stdin);
    freopen("convex.out", "w", stdout);

    scanf("%d", &n);
    For(i, 1, n) P[i].x = Read(), P[i].y = Read();
    For(i, 1, n - 1) assert(Cross(P[i + 1] - P[i], P[(i + 1) % n + 1] - P[i + 1]) < 0);
    reverse(P + 1, P + n + 1);
    For(i, 1, n) P[i + n] = P[i];
    For(i, 1, 2 * n) {
        sumx[i] = (sumx[i - 1] + P[i].x) % Mod;
        sumy[i] = (sumy[i - 1] + P[i].y) % Mod;
        if (i <= n) sums[i] = sums[i - 1] + Cross(P[i], P[i + 1]);
        s1[i] = sums[(i - 1) % n + 1] % Mod;
        if (i > n) s1[i] = (s1[i] + s1[n]) % Mod;
    }
    For(i, 1, 2 * n) s2[i] = (s2[i - 1] + s1[i]) % Mod;

    int pr = 1;
    int ans = 0;
    For(i, 1, n) {
        LL S = 0;
        while (pr + 1 < i + n && (S = -sums[i - 1] + (pr <= n ? sums[pr] : sums[pr - n] + sums[n]) + Cross(P[pr + 1], P[i])) < (sums[n] + 1) / 2) ++pr;
        if (sums[n] % 2 == 0 && S == sums[n] / 2 && (pr + 1) % n > i % n) ++pr;
        if (pr == i + 1) continue;
        ans = (ans + 1ll * s2[pr - 1] - s2[i] - 1ll * (pr - i - 1) * s1[i]) % Mod;
        ans = (ans + 1ll * (pr - i - 1) * (s1[i] - s1[i - 1])) % Mod;
        ans = (ans + 1ll * (sumx[pr] - sumx[i + 1]) * P[i].y - 1ll * (sumy[pr] - sumy[i + 1]) * P[i].x) % Mod;
    }
    ans = (1ll * n * (n - 3) / 2 % Mod * s1[n] - 2ll * ans) % Mod;
    ans = (ans + Mod) % Mod;
    printf("%d\n", ans);

    return 0;
}

2019雅礼集训 D7T3 convex [咕咕咕]

标签：NPU   for   printf   alt   数据   getch   题解   sig   bubuko   

原文地址：https://www.cnblogs.com/p-b-p-b/p/10261073.html