1059: [ZJOI2007]矩阵游戏

标签：ring   通过   交换操作   names   set   dinic   二分图   二分图匹配   zjoi   

Description

　　小Q是一个非常聪明的孩子，除了国际象棋，他还很喜欢玩一个电脑益智游戏——矩阵游戏。矩阵游戏在一个N*N黑白方阵进行（如同国际象棋一般，只是颜色是随意的）。每次可以对该矩阵进行两种操作：行交换操作：选择矩阵的任意两行，交换这两行（即交换对应格子的颜色）列交换操作：选择矩阵的任意行列，交换这两列（即交换对应格子的颜色）游戏的目标，即通过若干次操作，使得方阵的主对角线(左上角到右下角的连线)上的格子均为黑色。对于某些关卡，小Q百思不得其解，以致他开始怀疑这些关卡是不是根本就是无解的！！于是小Q决定写一个程序来判断这些关卡是否有解。

Too young too simple 的思想历程

1. 一共有n个黑子就一定有解!(...)

   (随便hack一下

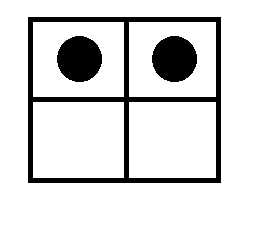
1. 每行都有黑子就有解！（。。。）

   （太蠢了不说了

2. 每行每列都有黑子就有解！

   还是不对啊！比如说

   

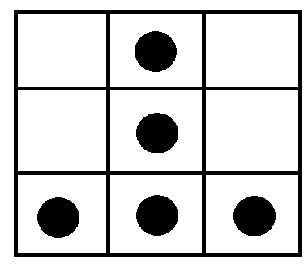
   就显然还是没解

3. 正解：存在n个点，x坐标和y坐标分别不相同

这里显然可以用二分图匹配！

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
#define M 1000001
using namespace std;

int t,m,n,k,d[M],ver[M],edge[M],nex[M],cnt,head[M],cur[M];
queue <int> q;
void add(int x,int y)
{
    ver[++cnt]=y; nex[cnt]=head[x]; head[x]=cnt; edge[cnt]=1;
    ver[++cnt]=x; nex[cnt]=head[y]; head[y]=cnt; edge[cnt]=0;
}

bool bfs()
{
    while(q.size()) q.pop();
    memset(d,0,sizeof(d)); memcpy(cur,head,sizeof(head));
    d[0]=1; q.push(0);
    while(q.size())
    {
        int x=q.front(); q.pop();
        for(int i=head[x];i;i=nex[i])
        if(!d[ver[i]] && edge[i])
        {
            d[ver[i]]=d[x]+1;
            if(ver[i]==t) return 1;
            q.push(ver[i]);
        }
    }
    return 0;
}

int dinic(int x,int flow)
{
    if(!flow || x==t) return flow;
    int re=flow, k;
    for(int& i=cur[x];i && re;i=nex[i])
    if(edge[i] && d[ver[i]]==d[x]+1)
    {
        k=dinic(ver[i],min(re,edge[i]));
        re-=k; edge[i]-=k; edge[i^1]+=k; 
    }
    return flow-re;
}

1059: [ZJOI2007]矩阵游戏

标签：ring   通过   交换操作   names   set   dinic   二分图   二分图匹配   zjoi   

原文地址：https://www.cnblogs.com/ZUTTER/p/10265895.html