用矩阵方式求解线性回归的最优θ

标签：图片   使用   表示   img   讲解   模型   最小二乘法   大数   预测   

1.假设回归的目标函数式为

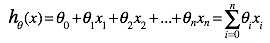
（其中x₀为1）

当 n = 1时表示一元函数，对一元函数进行回归分析

2.将误差记为：ε

要使得ε最小，然后样本真实值 y 和模型训练预测的值之间是有误差 ε ,再假设训练样本的数据量很大的时候,根据中心极限定律可以得到   ∑ε   满足 （u ,δ2）高斯分布的；由于方程有截距项 ，故使用可以 u =0; 故满足（0，δ2）的高斯分布；

如上面可知，对于每一个样本 x ,代入到 p (y |x ;θ) 都会得到一个y 的概率；又因为设定样本是独立同分布的；对其求最大似然函数：

对其化简如下：

对目标求解求偏导

以上就得到了回归的损失函数最小二乘法的公式，对于好多介绍一般对线性回归的线性损失函数就直接给出了上面的公式二乘法。下面我们就对上面做了阶段性的总结：线性回归，根据大数定律和中心极限定律假定样本无穷大的时候，其真实值和预测值的误差ε 的加和服从u=0,方差=δ2的高斯分布且独立同分布，然后把ε =y-?x 代入公式，就可以化简得到线性回归的损失函数；

    第二步：对损失函数进行优化也就是求出w,b，使的损失函数最小化；第一种方法使用矩阵（需要满足可逆条件）

 以上就是按矩阵方法优化损失函数，但上面方法有一定的局限性，就是要可逆；下面我们来说一说另外一个优化方法 梯度下降法；对于梯度下降法的说明和讲解资料很多，深入的讲解这里不进行，可以参考：http://www.cnblogs.com/ooon/p/4947688.html这篇博客，博主对梯度下降方法进行了讲解，我们这里就简单的最了流程解说;

W就是所求的参数θ矩阵。

用矩阵方式求解线性回归的最优θ

标签：图片   使用   表示   img   讲解   模型   最小二乘法   大数   预测   

原文地址：https://www.cnblogs.com/CK85/p/10276543.html