「CF86D」Powerful array 解题报告

标签：names   非递归   bit   space   ace   lin   数列   千万   有序   

题面

给出一个\(n\)个数组成的数列\(a\)，有\(t\)次询问，每次询问为一个\([l,r]\)的区间，求区间内每种数字出现次数的平方×数字的值 的和

思路：

直接上莫队咯 然后就T了

没学过莫队？！我也没办法

这道题的数据范围在\(2e5\)的级别，有人会问莫队肯定要炸啊 捏~

时限5000ms，那就可以乱搞了

但是！还是要加一些优化

如何优化？

1.对于算法本身的优化

由于莫队可以说是一个块状暴力的算法，就是把区间划分为\(\sqrt n\)块然后在块内暴力（到头还是暴力）

我们可以把要查询的区间当做点表示在平面直角坐标系上，RT：

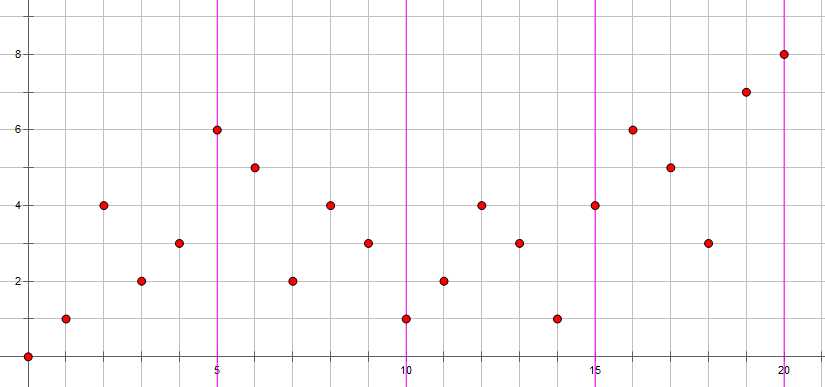
就像这样把询问放在平面直角坐标系上，\(\large x\)轴为询问该区间的顺序，\(\large y\)轴表示该区间的右端点，如果我们忽略区间的\(L\)值的影响，不难看出，虽然我们已经把区间划分在一个块里了，但是还是有很多冗余的操作，如果要是这些冗余的操作少一点就好了，这当然可以啦！

我们可以让块内的区间按\(\large R\) 递增，这样能省很多时间，但是在区间过渡的时候，我们还是会做很多多余的操作，因为区间都是递增的，这样改变块的时候就可能有一个很大的落差，就掉了下去，可以自己想象一下

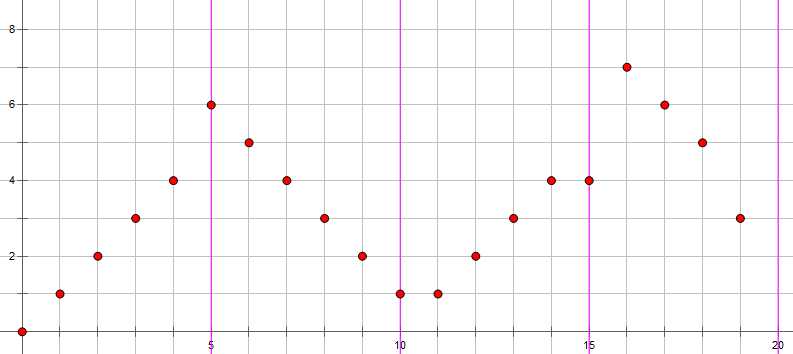
为了避免上述的现象，我们可以让区间像一个波浪一样，这样就很高效了，这样的划分方式叫做奇偶划分应该是这么叫的吧，还有一个是奇偶性剪枝

inline bool cmp(node a,node b){//代码是关键，讲了啥不重要(手动划线)
    return (pos[a.l]==pos[b.l])?(pos[a.l]&1)?a.r<b.r:a.r>b.r : a.l<b.l;
}//千万不要写if，会T！

接着就是块的大小，同样影响速度，一般普通的块的大小应该是\(\large \sqrt n\)，但是，根据某奆佬研究，大小为\(\large n^{0.54}\)时更快，Orz

2.对于程序本身优化，说人话就是卡卡常

比如：

加点register

非递归函数前加个inline

不用快读用fread

还有！乘法变加法……

然后就把最大时间卡到了622ms

啊哈哈哈哈哈

Code：

#include<bits/stdc++.h>
#define getchar() *(p++)//在快读基础上改一点就行了
#define Re register//卡常必备
#define ll long long
#define M 1000010
#define N 200010
using namespace std;
struct node{
    int l,r,i;
}b[N];//sum是数的多少，pos表示在哪块
int a[N],pos[N],n,m,sum[M],l,r,block;
ll Ans[N],ans;
char bf[1<<25],*p;
int read(){
    Re int s=0;
    Re char c=getchar();
    while(!isdigit(c))
        c=getchar();
    while(isdigit(c))
    {
        s=(s<<1)+(s<<3)+c-'0';
        c=getchar();
    }
    return s;
}
inline bool cmp(node a,node b){//奇偶划分
    return (pos[a.l]==pos[b.l])?(pos[a.l]&1)?a.r<b.r:a.r>b.r : a.l<b.l;
}//注意，这里不要写if语句，会T
inline void Add(Re ll x)
{
    sum[x]++;//有些人写在前面，那样的话就应该是+1
    ans+=(sum[x]+sum[x]-1)*x;//就是由原来的乘变成了加，手算一小部分也没有关系啦
}
inline void Del(Re ll x)
{
    ans-=(sum[x]+sum[x]-1)*x;//这里和上面也是一样的
    sum[x]--;//为什么我感觉上面-1会更慢呢~
}
int main()
{
    Re int i;
    bf[fread(bf,1,1<<25,stdin)]='\0';p=bf;//fread大法
    n=read();m=read();block=pow(n,0.54);//神奇的块的大小
    for(i=1;i<=n;i++)
        a[i]=read(),pos[i]=i/block;
    for(i=1;i<=m;i++)
        b[i].l=read(),b[i].r=read(),b[i].i=i;
    sort(b+1,b+1+m,cmp);l=1;
    for(i=1;i<=m;i++)//然后上莫队
    {
        while(r<b[i].r)
            Add(a[++r]);
        while(r>b[i].r)
            Del(a[r--]);
        while(l<b[i].l)
            Del(a[l++]);
        while(l>b[i].l)
            Add(a[--l]);
        Ans[b[i].i]=ans;
    }
    for(i=1;i<=m;i++)
        printf("%lld\n",Ans[i]);
    return 0;
}

再说一遍

最后注意，sort的时候，如果数组本来就有序了，sort会很慢，所以千万不要在里面加if了，容易T

「CF86D」Powerful array 解题报告

标签：names   非递归   bit   space   ace   lin   数列   千万   有序   

原文地址：https://www.cnblogs.com/hovny/p/10287471.html