标签:直接 删除 树根 文献 产生 排序 com 详解 概念
具体讲解之前,有一点,再次强调下:B-树,即为B树。因为B树的原英文名称为B-tree,而国内很多人喜欢把B-tree译作B-树,其实,这是个非常不好的直译,很容易让人产生误解。如人们可能会以为B-树是一种树,而B树又是一种树。而事实上是,B-tree就是指的B树。特此说明。
m阶B树的M阶指的是所有节点中的子节点个数的最大值。
(1)节点最多有m个分支。
(2)根节点最少有两个分支,非根非叶节点至少有ceil(m/2)个分支。
(3)节点内关键字递增排序。
(4)一个节点有n-1个关键字,则该节点有n个分支,将关键字一一隔开。
(5)节点中任何一个关键字,其左边分支上的节点值都小于这个关键字,右边分支的节点值都大于这个关键字。
(6)叶子节点处于同一层。
如图5阶B树满足:
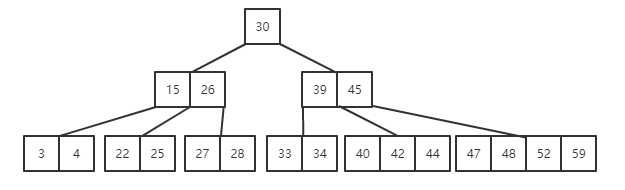
(1)节点最多有5个分支(叶子节点)。
(2)根节点最少有两个分支,非根非叶节点至少有3个分支。
(3)节点内关键字递增排序。
(4)一个节点有2个关键字,则该节点有2+1个分支,将关键字一一隔开。
(5)节点中任何一个关键字,其左边分支上的节点值都小于这个关键字,右边分支的节点值都大于这个关键字。
(6)叶子节点处于同一层。
由上可知,m阶B树,非根非叶节点至少有ceil(m/2)个分支,最多由m个分支,则节点关键字个数的范围为ceil(m/2)-1 ~ m-1。
B树节点的插入是待插入节点的值与B树节点依次比较的过程,从根节点开始,若小于当前节点的值,则递归与节点的左子树进行比较,若大于则与右子树进行比较。由此可见,B树节点的插入总是落在叶子节点上,在插入过程中可能会破坏B树的特征,如新关键字的插入使得节点中关键字的个数超过规定个数,则要进行节点拆分。
我们以关键字序列{1,2,6,7,11,4,8,13,10,5,17,9,16,20,3,12,14,18,19,15}创建一个5阶B树。
(1)确定节点关键字个数范围,由于创建的是5阶B树,因此关键字的个数范围为2~4。
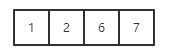
(2)根结点最多可以容纳4个关键字,依次插入关键字1、2、6、7
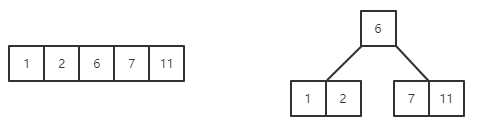
(3)插入关键字11,发现此时结点中关键字的个数变为5,超出范围,需要拆分,去关键字数组中的中间位置,也就是k[3]=6,作为一个独立的结点,即新的根结点,将关键字6左、右关键字分别做成两个结点,作为新根结点的两个分支(图左为拆分前,图右为拆分后)
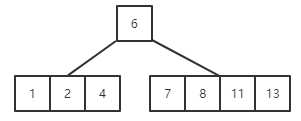
(4)新关键字总是插在叶子结点上,插入关键字4、8、13
(5)关键字10需要插入在关键字8和11之间,此时又会出现关键字个数超出范围的情况,因此需要拆分。拆分时需要将关键字10纳入根结点中,并将10左右的关键字做成两个新的结点连在根结点上。

(6)插入关键字5、17、9、16
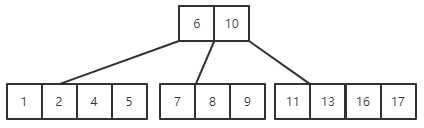
(7)关键字20插入在关键字17以后,此时会造成结点关键字个数超出范围,需要拆分,方法同上

(8)按照上述步骤依次插入关键字3、12、14、18、19
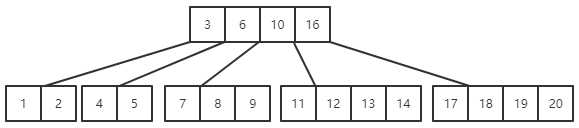
(9)插入最后一个关键字15,15应该插入在14之后,此时会出现关键字个数超出范围的情况,则需要进行拆分,将13并入根结点,13并入根结点之后,又使得根结点的关键字个数超出范围,需要再次进行拆分,将10作为新的根结点,并将10左、右关键字做成两个新结点连接到新根结点的指针上,这种插入一个关键字之后出现多次拆分的情况称为连锁反应

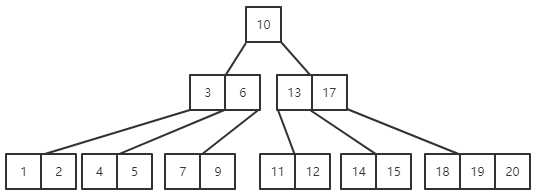
(2)删除关键字15,15虽然也在终端结点上,但是不能直接删除,因为删除后当前结点中关键字的个数小于2。这是需要向其兄弟结点借关键字,显然应该向其右兄弟来借关键字,因为左兄弟的关键字个数已经是下限2.借关键字不能直接将18移到15所在的结点上,因为这样会使得15所在的结点上出现比17大的关键字,所以正确的借法应该是先用17覆盖15,在用18覆盖原来的17,最后删除原来的18。
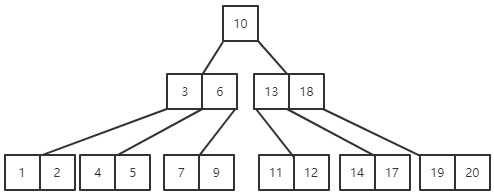
(3)删除关键字4,4在终端结点上,但是此时4所在的结点的关键字个数已经到下限,需要借关键字,不过可以看到其左右兄弟结点已经没有多余的关键字可借。
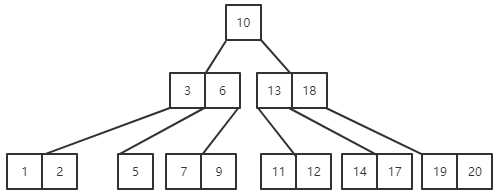
所以就需要进行关键字的合并。可以先将关键字4删除,然后将关键字5、6、7、9进行合并作为一个结点链接在关键字3右边的指针上,也可以将关键字1、2、3、5合并作为一个结点链接在关键字6左边的指针上.

显然上述两种情况下都不满足B-树的规定,即出现了非根的双分支结点,需要继续进行合并。

标签:直接 删除 树根 文献 产生 排序 com 详解 概念
原文地址:https://www.cnblogs.com/yfzhou/p/10290006.html