标签:移动 二分 相关 线性规划 两种 play 独立 一段 直线
当遇到类似:\(f[i] = \sum_{j = k}^{i} g[j]\)的转移时,可以通过预处理出\(g[i]\)的前缀和\(s[i]\),将\(O(n)\)的求和转换为\(O(1)?\)的操作。
[HAOI2008]木棍分割 二分答案+dp
P4099 [HEOI2013]SAO 树形dp
接下来几种优化方法主要是对1d/1d dp的优化,其中xd/yd dp指的是状态数有\(n^x\)种,每个状态的转移有\(n^y\)种的dp。对于1d/1d dp,我们可以写出其转移的通式:\(f[i] = min/max\{f[j] + w(i, j)\}\),其暴力转移是\(O(n^2)\)级别的,我们希望能够通过式子的某些特殊性来优化转移。
接下来我们会考察三种式子,第一种式子形如:
\[
f[i] = min_{j = i - d}^{i - 1}\{f[j] + w(j) + w(i)\}
\]
我们可以看到这一类式子的特点:
1.对于i的转移,其决策点是一段连续的区间,并且这个区间随着i的右移而单调右移。
2.每次转移的代价\(w(i,j)?\)中,i与j的花费相互独立。
那么,首先考察两个决策\(j\)与\(k\)(\(j<k\)),如果决策\(k\)优于\(j\),那么对于决策\(i‘\)(\(i‘>i\)),从\(k\)转移一定更优,\(j\)一定不再会成为最优决策。也就是说,我们的决策是单调的,我们称这样的方程满足决策单调性。那么,我们只需要维护一个单调队列,维护队列中的决策单增/单减,对于转移\(i\),首先检查队头元素是否还属于合法的转移区间\([i - d, i - 1]\),如果不合法则pop_front()。由于单调队列的单调性,此时的队头就是最优决策,进行转移。接着,更新决策区间,维护单调性,将新的决策点从队尾加入单调队列。
关于单调队列优化有一个非常经典的算法——单调队列优化多重背包:
首先我们知道多重背包的方程:\(f[i][j] = max\{f[i -1][j], f[i - 1][j - k * w[i]] + c[i] *k\}\)。我们单独关注后面的部分,多重背包复杂度\(O(nmk)\)就在于最后枚举每件物品的个数,如果用二进制拆分可以将复杂度优化到\(O(nmlogk)\)。但是,如果我们想要进一步提高效率,我们就会用到单调队列优化多重背包。
首先,我们把式子改写成可以单调队列优化的形式:首先,对于重量为\(w\),价值为\(c\)的物品,令\(j=nw+p\),则原方程可以写成\(f[i][j] = max\{f[i -1][j], f[i - 1][p + k * w[i]] - c[i] *k+ c[i] * n\}, p \in[0,w]\),这个式子已经被调整为单调队列优化的式子了,对于每个物品先枚举mod w后的余数,在单调队列里维护\(f[i - 1][p + k * w[i]] - c[i] *k\)递增即可。
宝物筛选 单调队列优化多重背包
考察的第二种式子形如:
\[
f[i] = min\{f[j] + w(i,j)\}
\]
且要求这一类式子具有以下特点:
1.w(i,j)展开后能得到关于\(i、j\)的乘积项,经过调整能够化成形如\(\frac{y1-y2}{x1-x2}\)的斜率式
2.具有决策单调性
那么首先来考虑一个一般性的方程\(f[i] = min\{a[i]\times b[j] + c[i] + d[j]\}(a,b,c,d >0且b单增)\),其中\(a[i]\times b[j]\)就是我们所说的关于\(i,j\)的乘积项。对于状态\(i\)我们考察他的决策,那么我们可以先把方程化为以\(j\)的相关项为自/因变量,即:
\[
-d[j] = a[i]\times b[j] + c[i] - f[i]
\]
我们将这个式子对应回直线的斜截式\(y=kx+b?\)有\(y=-d[j], x = b[j], k = a[i], b = c[i] -f[i]?\),我们希望最小化\(f[i]?\),那么也就是要最大化\(b?\),由于斜率\(k?\)是一定的,那么我们考虑进行线性规划,将每个决策\(j?\)对应到座标系上,直线与这些决策点形成的凸包相切时可以取到\(b?\)的最值,由于我们要的是\(b?\)的最大值且\(k=a[i]>0?\),那么直线要和凸包上切,换言之,我们只需要维护这些决策点形成一个下凸包即可。
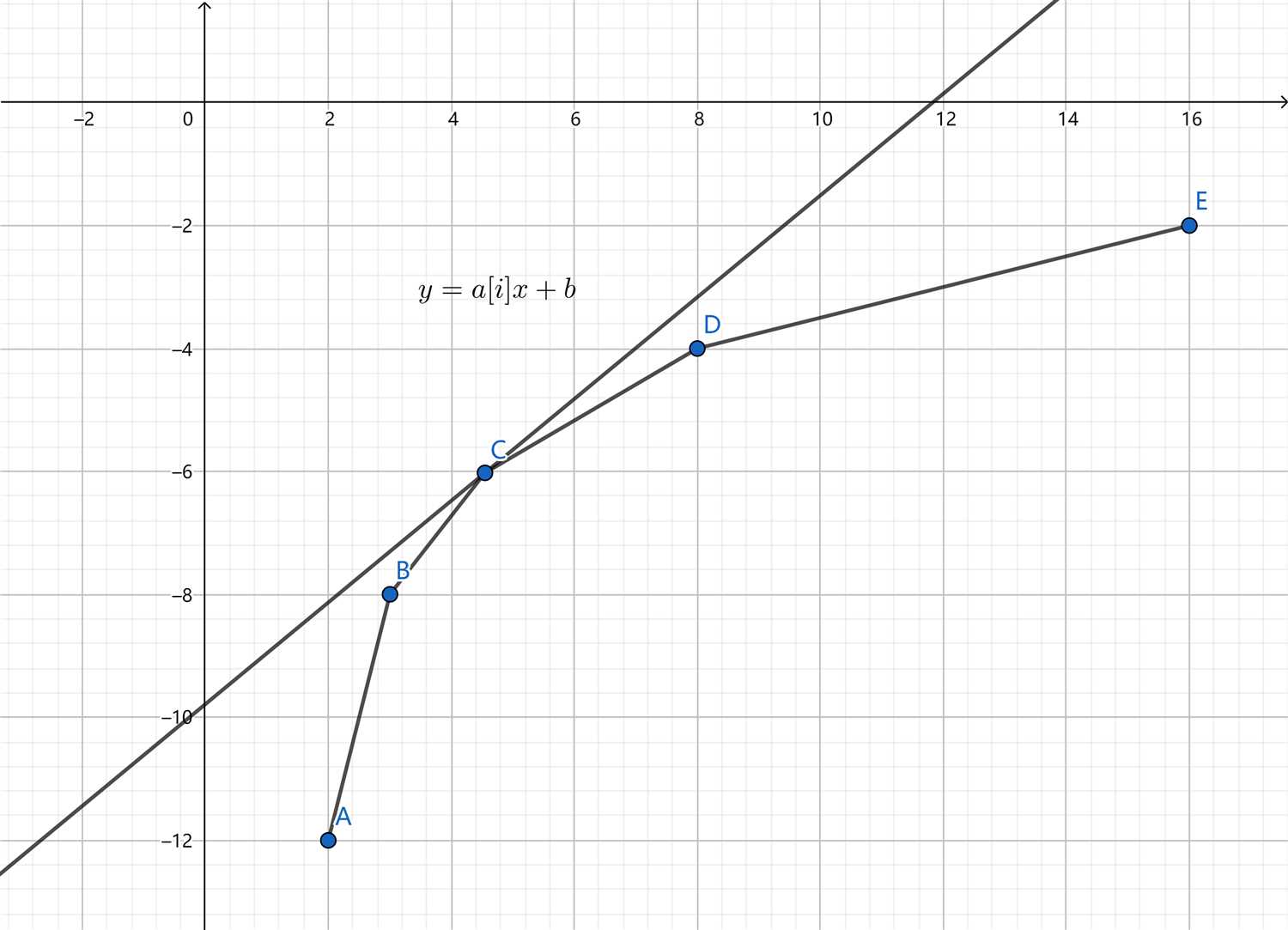
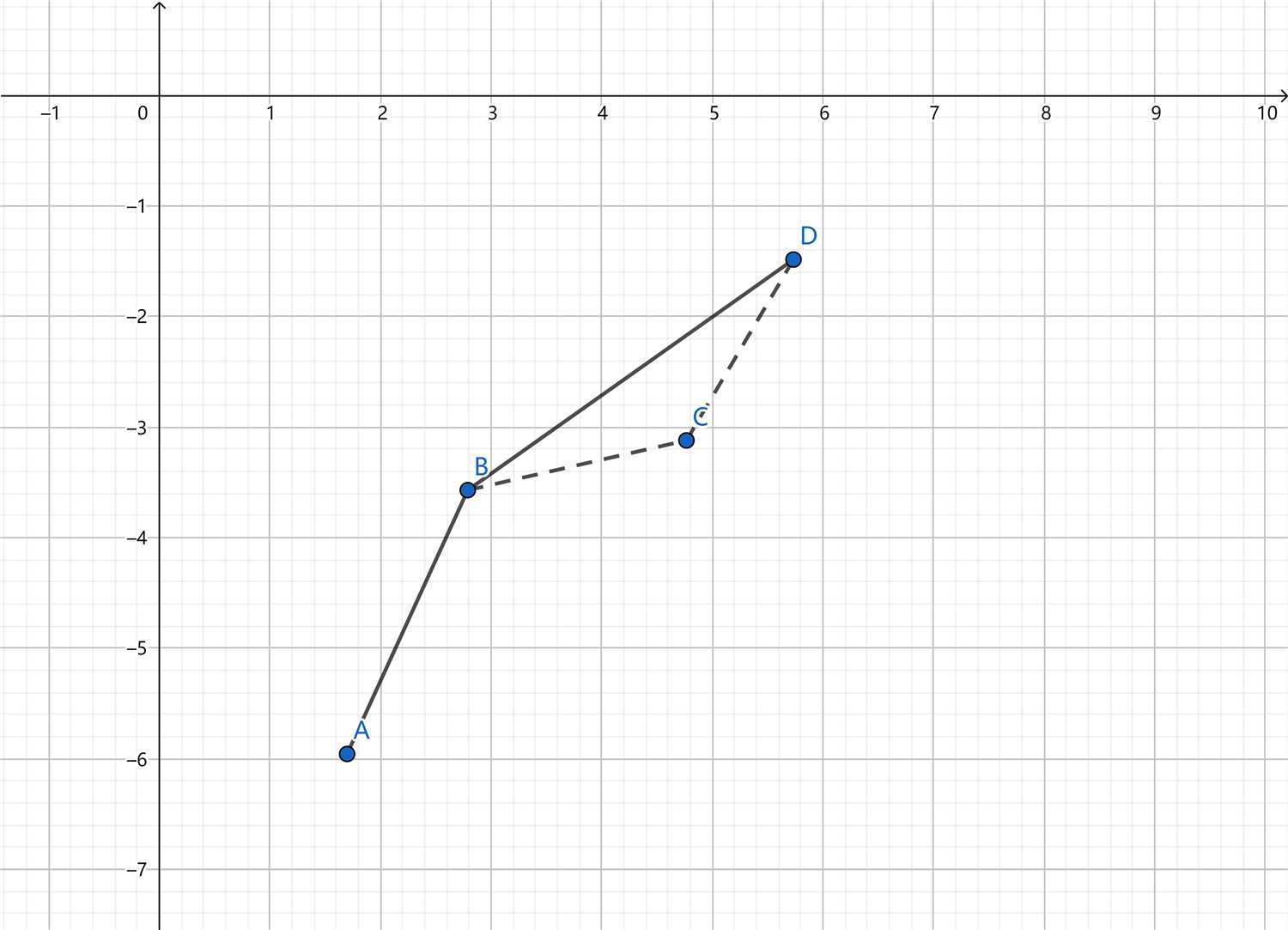
接下来考虑如何维护这个上凸包,凸包斜率单调减,那么我们依然可以用单调队列维护,新加入一个决策\(i?\)时,先与队尾比较,判断是否满足\(slope(i, q[t]) <slope(q[t], q[t - 1])?\),如果满足直接加入,否则,则如下图\(k_{DC} > k_{BC}?\),说明此刻\(C?\)一定不会出现在之后的最优策略里(不可能成为直线切点),那么我们pop_back()掉队尾即可。
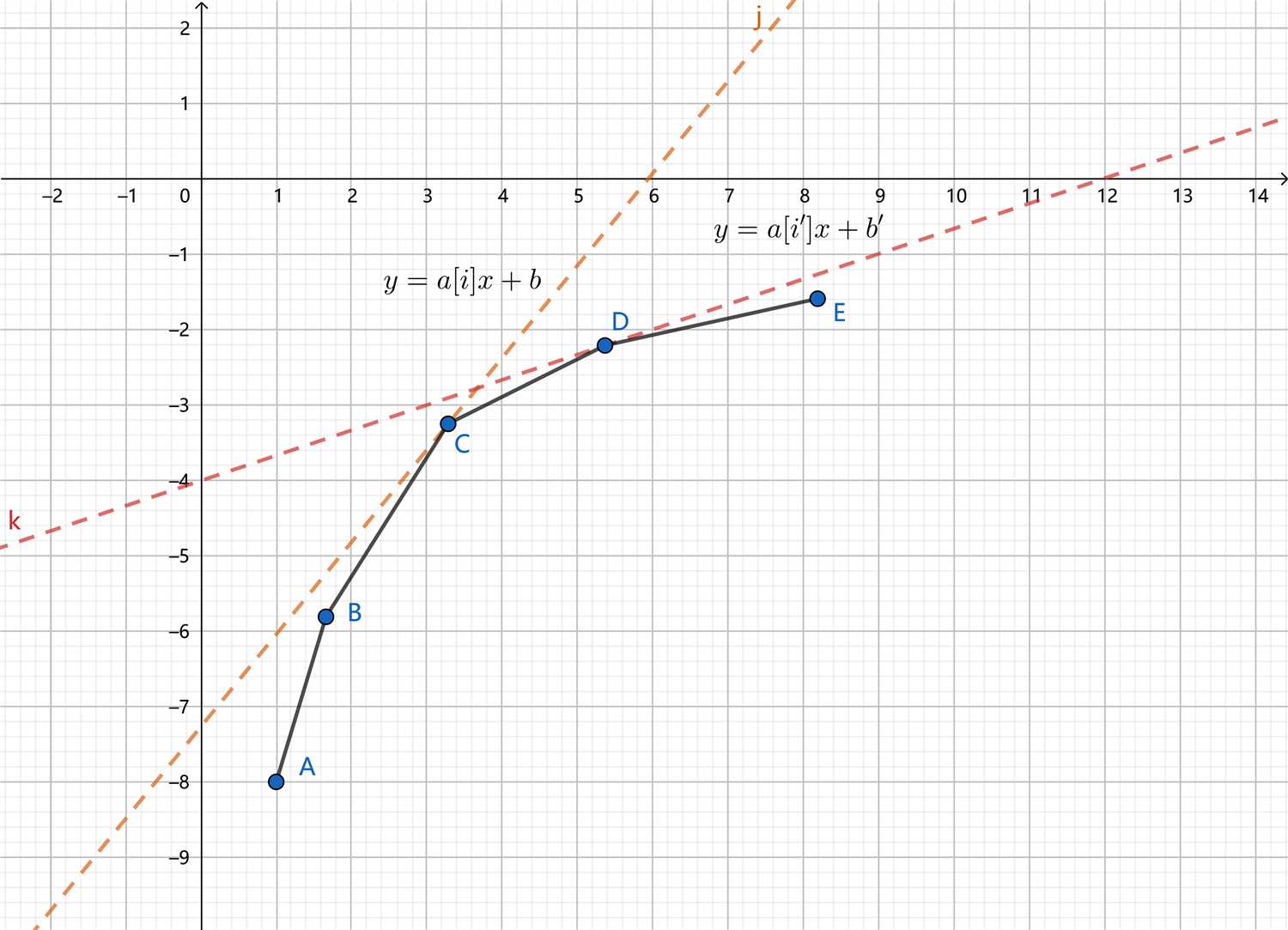
现在单调队列里维护了决策凸包,接着我们每次转移的时候如何在凸包中选出最优决策呢?如果我们的斜率\(k=a[i]?\)是单调的(以单减为例),对于\(i‘>i有a[i‘]<a[i]?\)且i的最优决策点\(C?\),由于决策单调性\(i‘?\)的决策一定会是\(C?\)往后的决策。或者总图形的角度说,如下图,有\(k_{AB} > k_{BC} > k_{CD} >a[i‘]?\),决策A、B、C一定都不是优的。综上,若\(a[i] < k(q[h], q[h - 1])?\)时,决策\(q[h]?\)一定不优,pop_front()到\(q[h]?\)最优即可,这样暴力移动队首指针可以将复杂度优化到\(O(n)?\)
如果斜率不单调,那么我们可以通过在凸包上二分将复杂度优化成\(O(nlogn)\)。在开始的式子\(f[i] = min\{a[i]\times b[j] + c[i] + d[j]\}(a,b,c,d >0且b单增)\)中有个条件:b单增。这个条件也就是决策点的x单增,使得我们能够用单调队列维护凸包。如果b不单增时,我们则必须通过CDQ分治或者平衡树来维护凸包。
最后补充另一种理解斜率优化,判断决策单调性的方法,依然对于式子\(f[i] = min\{a[i]\times b[j] + c[i] + d[j]\}\) ,我们假设有决策\(j,k(j<k)\)且\(k?\)优于$j,则有:
\[
a[i]\times b[j] + c[i] + d[j] > a[i]\times b[k] + c[i] + d[k]
\]
\[ 即:a[i]\times (b[j] - b[k]) > d[k]-d[j] \]
\[ \frac{-d[k] - (-d[j])}{b[k]-b[j]}>a[i] \]
这样就得到了决策优劣判断的关系式了,具体含义理解应对回前面的几何意义即可。
[NOI2007]货币兑换 斜优+CDQ分治
高速公路 可持久化数组+斜优/斜优+二分
考察的第三种式子依然形如:
\[
f[i] = min\{f[j] + w(i,j)\}
\]
一般来说这一类式子的\(w(i,j)?\)已经不像前两种情况下那么独立了,譬如\(\sqrt{\mid a[i]-a[j] \mid}, (a[i] - a[j])^p?\)等等。但是,如果转移依然满足决策单调性了话,我们便能够将其优化成\(O(nlogn) ?\)
在某些转移中(例如枚举左右端点),方程中的两维i与j存在类似于\(s[i]+s[j]<val?\)的限制条件,并且我们知道\(s[i]?\)与\(s[j]?\)都是单增的,那么当我们左移i指针时\(s[i]\uparrow,s[j]\downarrow?\),则j指针只能够向右移动。这样,我们可以通过调整指针移动的顺序和方向将二维的枚举优化成一维。
[AH2017/HNOI2017]大佬 dp+bfs
标签:移动 二分 相关 线性规划 两种 play 独立 一段 直线
原文地址:https://www.cnblogs.com/grannychan/p/10295567.html