标签:也会 而且 图片 公式 span class 使用 play 部分
所有的RNN都具有一种重复神经网络模块的链式形式。在标准RNN中,这个重复的结构模块只有一个非常简单的结构,例如一个tanh层
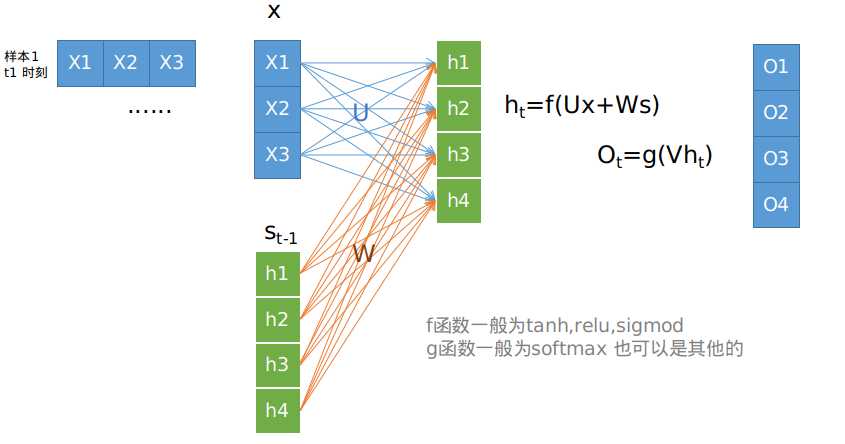
在时间视角上的显示为下图:

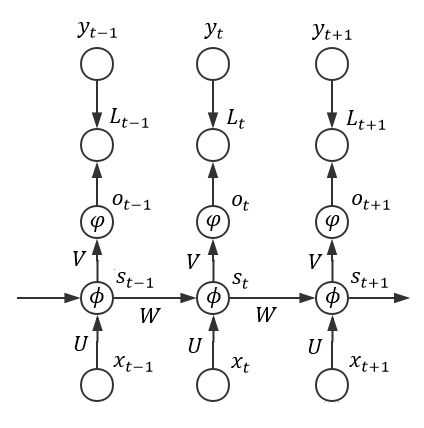
整体误差E等于每个时刻E_t的误差之和
整体损失对U/V/W进行求偏导
\[
ΔU=\frac{\partial E}{\partial U}=\sum_t \frac{\partial e_t}{\partial U}
\]
\[
ΔV=\frac{\partial E}{\partial V}=\sum_t \frac{\partial e_t}{\partial V}
\]
\[
ΔW=\frac{\partial E}{\partial W}=\sum_t \frac{\partial e_t}{\partial W}
\]
ΔU 求导:对于Ot=g(V*St) 求ΔU是简单的,St是输出值已知,不依赖之前的状态,可以直接求导每一个时刻的 ΔW 求导:Wt 不仅影响Et, 而且也会印象到Et+1(因为在计算Et+1的使用包含St的值),并且Wt-1 也会印象到Et+1.
例如t+1时刻的误差Et+1,我们去计算w1,w2...wt+1的梯度值
\[
\frac{\partial e_{t+1}}{\partial W^{t+1}}= \frac{\partial e_{t+1}}{\partial h^{t+1}} \frac{\partial h_{t+1}}{\partial W^{t+1}}
\]
\[ \frac{\partial e_{t+1}}{\partial W^{t}}= \frac{\partial e_{t+1}}{\partial h^{t+1}} \frac{\partial h_{t+1}}{\partial h^{t}}\frac{\partial h_{t}}{\partial W^{t}} \]
\[ \frac{\partial e_{t+1}}{\partial W^{t-1}}= \frac{\partial e_{t+1}}{\partial h^{t+1}} \frac{\partial h_{t+1}}{\partial h^{t}}\frac{\partial h_{t}}{\partial h^{t-1}}\frac{\partial h_{t-1}}{\partial w^{t-1}} ...... \]
因为RNN中的参数值是共享的 所以Wt=Wt-1=Wt-2 ,同理其他参数也是一样的,所以计算上述公式时就可以抹去标签并求和了。
? 因为有符合函数求导公式
\[
f(x)=g(x)h(x)
\text{求导得}
\frac{\partial f}{\partial x}=\frac{\partial g}{\partial x}*h+\frac{\partial h}{\partial x}*g
\]
\[ \text{原函数:} h_{t+1}=f(Ux+W_{t+1}h_t) \]
其中Ux不包含W,可以不用考虑,当做常数,f 是一个整体转化 可以忽略成 Ht+1=Ht*Wt+1其中包含两部分Ht和Wt+1,依照上面的两个函数求导法制。
\[ \frac{\partial e_{t+1}}{\partial W^{t+1}}= \frac{\partial e_{t+1}}{\partial h^{t+1}} *h^t \]
\[ \frac{\partial e_{t+1}}{\partial W^{t}}= \frac{\partial e_{t+1}}{\partial h^{t+1}} *W*h^{t-1} \]
\[ \frac{\partial e_{t+1}}{\partial W^{t-1}}= \frac{\partial e_{t+1}}{\partial h^{t+1}}*W*W*h^{t-2} \]
将上述式子求和得
\[
\frac{\partial e_t}{\partial W}= \sum_{k=1}^t\frac{\partial e_t}{\partial h^t}\prod_{i=k}^t\frac{\partial h_i}{\partial h^{i-1}}\frac{\partial ^+ h_k}{\partial W}
\]
其中下式 表示不进行链式求导,将其他参数都看做常数,直接进行求导。
\[
\frac{\partial ^+ h_k}{\partial W}
\]
标签:也会 而且 图片 公式 span class 使用 play 部分
原文地址:https://www.cnblogs.com/zhuimengzhe/p/10300738.html